
【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2 ![]() ),点B在x轴的正半轴上,点E为线段AD的中点
),点B在x轴的正半轴上,点E为线段AD的中点
(1)如图1,求∠DAO的大小及线段DE的长;
(2)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3 ![]() .
.
①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).
【答案】
(1)解:∵A(﹣2,0),D(0,2 ![]() )
)
∴AO=2,DO=2 ![]() ,
,
∴tan∠DAO= ![]() =
= ![]() ,
,
∴∠DAO=60°,
∴∠ADO=30°,
∴AD=2AO=4,
∵点E为线段AD中点,
∴DE=2;
(2)解:①如图2,

过点E作EM⊥CD,
∴CD∥AB,
∴∠EDM=∠DAB=60°,
∴EM=DEsin60°= ![]() ,
,
∴GH=6,
∵CD∥AB,
∴∠DGE=∠OFE,
∵△OEF′是△OEF关于直线OE的对称图形,
∴△OEF′≌△OEF,
∴∠OFE=∠OF′E,
∵点E是AD的中点,
∴OE= ![]() AD=AE,
AD=AE,
∵∠EAO=60°,
∴△EAO是等边三角形,
∴∠EOA=60°,∠AEO=60°,
∵△OEF′≌△OEF,
∴∠EOF′=∠EOA=60°,
∴∠EOF′=∠AEO,
∴AD∥OF′,
∴∠OF′E=∠DEH,
∴∠DEH=∠DGE,
∵∠DEH=∠EDG,
∴△DHE∽△DEG,
∴ ![]() ,
,
∴DE2=DG×DH,
设DG=x,则DH=x+6,
∴4=x(x+6),
∴x1=﹣3+ ![]() ,x2=﹣3﹣
,x2=﹣3﹣ ![]() ,
,
∴DG=﹣3+ ![]() .
.
②如图3,
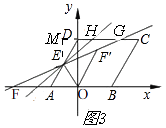
过点E作EM⊥CD,
∴CD∥AB,
∴∠EDM=∠DAB=60°,
∴EM=DEsin60°= ![]() ,
,
∴GH=6,
∵CD∥AB,
∴∠DHE=∠OFE,
∵△OEF′是△OEF关于直线OE的对称图形,
∴△OEF′≌△OEF,
∴∠OFE=∠OF′E,
∵点E是AD的中点,
∴OE= ![]() AD=AE,
AD=AE,
∵∠EAO=60°,
∴△EAO是等边三角形,
∴∠EOA=60°,∠AEO=60°,
∵△OEF′≌△OEF,
∴∠EOF′=∠EOA=60°,
∴∠EOF′=∠AEO,
∴AD∥OF′,
∴∠OF′E=∠DEH,
∴∠DEG=∠DHE,
∵∠DEG=∠EDH,
∴△DGE∽△DEH,
∴ ![]() ,
,
∴DE2=DG×DH,
设DH=x,则DG=x+6,
∴4=x(x+6),
∴x1=﹣3+ ![]() ,x2=﹣3﹣
,x2=﹣3﹣ ![]() ,
,
∴DH=﹣3+ ![]() .
.
∴DG=3+ ![]()
∴DG=AF=3+ ![]() ,
,
∴OF=5+ ![]() ,
,
∴F(﹣5﹣ ![]() ,0)
,0)
【解析】(1)根据点A的坐,点D的坐标,在Rt△AOD中,利用解直角三角形易求出结论。
(2)①由(1)可知∠DAO=60°,添加辅助线,过点E作EM⊥CD,利用解直角三角形可求出EM、GH的长,根据已知易证明△OEF′≌△OEF,可得出角相等,点E是AD的中点,易得到△EAO是等边三角形,再证明△DHE∽△DEG,得出对应边成比例,设DG=x,则DH=x+6,建立方程,求出方程的解即可;②要求点F的坐标,就需求OF的长,解法与①类似求出DG,DG=AF,即可求出OF的长,从而求出点F的坐标。
【考点精析】通过灵活运用平行四边形的性质和相似三角形的判定与性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲乙两种型号的设备可供选购,经调查:购买
台节省能源的新设备,现有甲乙两种型号的设备可供选购,经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲乙两种型号设备的价格;
(2)该公司决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备的资金不超过
台,预算购买节省能源的新设备的资金不超过![]() 万元,你认为该公司有那几种购买方案?
万元,你认为该公司有那几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2018为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC= °;
(2)如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;
(3)如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE=![]() ∠CDN,∠CBE=
∠CDN,∠CBE=![]() ∠CBM),试求∠E的度数.
∠CBM),试求∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格纸中,小正方形的顶点叫做格点,![]() 是一个格点三角形(即
是一个格点三角形(即![]() 的三个顶点都在格点上),根据要求回答下列问题:
的三个顶点都在格点上),根据要求回答下列问题:

(1)画出![]() 先向右平移6格,再向下平移2格所得的
先向右平移6格,再向下平移2格所得的![]() ;
;
(2)过点B画直线![]() ,将
,将![]() 分成面积相等的两个三角形;
分成面积相等的两个三角形;
(3)![]() 的面积是 ;
的面积是 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.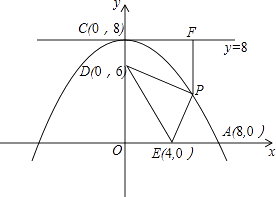
(1)求抛物线的解析式;
(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值?如果是,请求出此定值;如果不是,请说明理由;
(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前我市“校园手机”现象越来越受到社会关注,针对这种现象,重庆一中初三(1)班数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对),并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)根据抽样调查结果,请你估计我校11000名中学生家长中有多少名家长持反对态度;
(4)在此次调查活动中,初三(1)班和初三(2)班各有2位家长对中学生带手机持反对态度,现从中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加学校举办的“新城杯”足球联赛,新城中学七(1)班学生去商场购买了A品牌足球1个、B品牌足球2个,共花费400元,七(2)班学生购买了品牌A足球3个、B品牌足球1个,共花费450元.
(1)求购买一个A种品牌、一个B种品牌的足球各需多少元?
(2)为了进一步发展“校园足球”,学校准备再次购进A、B两种品牌的足球,学校提供专项经费850元全部用于购买这两种品牌的足球,学校这次最多能购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y1=a(x﹣2)2+c(a≠0)的图象与y轴的交点为(0,1),在x轴上截得的线段长为 ![]() .
.
(1)求a、c的值.
(2)对于任意实数k,规定:当﹣2≤x≤1时,关于x的函数y2=y1﹣kx的最小值称为k的“贡献值”,记作g(k).求g(k)的解析式.
(3)在(2)条件下,当“贡献值”g(k)=1时,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com