练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一个二次函数图像上部分点的横坐标，纵坐标的对应值如下表：

    …

    -4

    -3

    -2

    -1

    0

    1

    2

    3

    4

    …

    …

    0

    2

    0

    -6

    …

    （1）的值为______；

    （2）在给定的直角坐标系中，画出这个函数的图像；

    （3）当时，求的取值范围.

    【答案】（1）m=；（2）图像见解析；（3）-6＜y≤2

    【解析】

    （1）由x=-3与x=1时y值一样可得到，函数的对称轴为x=-1，所以x=2的函数值与x=-4的函数值一样，即可得到m；（2）利用五点作图法画出图形即可；（3）根据函数图像结合表格直接读出y的取值范围即可.

    （1）由x=-3与x=1时y值一样可得到，函数的对称轴为x=-1，所以x=2的函数值与x=-4的函数值一样，由表可知x=-4时，y=，故m=

    （2）图像如下图

    （3）由图像可知时，x=3时y值最小，x=-1时y值最大，

    故时，-6＜y≤2

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某中学开展“头脑风暴”知识竞赛活动，八年级班和班各选出名选手参加初赛，两个班的选手的初赛成绩（单位：分）分别是：

    1班85 80 75 85 100

    2班80 100 85 80 80

    （1）根据所给信息将下面的表格补充完整；

    平均数

    中位数

    众数

    方差

    班初赛成绩

    班初赛成绩

    （2）根据问题（1）中的数据，判断哪个班的初赛成绩较为稳定，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：

    在平面直角坐标系xOy中，点P（x0，y0）到直线Ax+By+C=0的距离公式为：．

    例如：求点P0（0，0）到直线4x+3y﹣3=0的距离．

    解：由直线4x+3y﹣3=0知，A=4，B=3，C=﹣3，∴点P0（0，0）到直线4x+3y﹣3=0的距离为=．

    根据以上材料，解决下列问题：

    问题1：点P1（3，4）到直线的距离为 ；

    问题2：已知：⊙C是以点C（2，1）为圆心，1为半径的圆，⊙C与直线相切，求实数b的值；

    问题3：如图，设点P为问题2中⊙C上的任意一点，点A，B为直线3x+4y+5=0上的两点，且AB=2，请求出S△ABP的最大值和最小值．

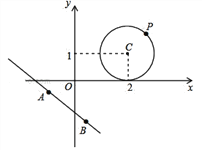
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面内的两条直线l1、l2,点A、B在直线l2上，过点A、B两点分别作直线l1的垂线，垂足分别为A1、B1，我们把线段A1B1叫做线段AB在直线l2上的正投影，其长度可记作T（AB，CD）或T（AB，l2）,特别地，线段AC在直线l2上的正投影就是线段A1C，请依据上述定义解决如下问题.

    （1）如图1，在锐角△ABC中，AB=5，T（AC，AB）=3，则T（BC，AB）= ；

    （2）如图2，在Rt△ABC中，∠ACB=90°，T（AC，AB）=4，T（BC，AB）=9，求△ABC的面积；

    （3）如图3，在钝角△ABC中，∠A=60°，点D在AB边上，∠ACD=90°，T（AD，AC）=2，T（BC，AB）=6，求T（BC，CD）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某淘宝网店销售台灯，成本为每个30元．销售大数据分析表明：当每个台灯售价为40元时，平均每月售出600个；若售价每下降1元，其月销售量就增加200个．

    （1）若售价下降1元,每月能售出 个台灯，若售价下降x元(),每月能售出 个台灯．

    （2）为迎接“双十一”，该网店决定降价促销，在库存为1210个台灯的情况下，若预计月获利恰好为8400元，求每个台灯的售价．

    （3）月获利能否达到9600元，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，对于点，如果点的纵坐标满纵坐标满足： ，那么称点为点的“关联点”.

    （1）请直接写出点的“关联点”的坐标____________；

    （2）若点在函数的图像上，其“关联点”与点重合，求点的坐标；

    （3）若点的“关联点”在函数的图像上，当时，求线段的最大值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

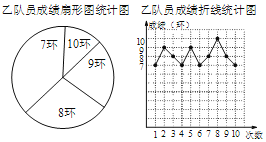
    【题目】某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛，特为甲、乙两名队员单行了一次选拔赛，要求这两名队员各射击10次，比赛结束后，根据比赛成绩情况，将甲，乙两名队员的比赛成绩制成了如下的统计图（表）：

    甲队员的成绩统计表：

    成绩（单位：环）

    7

    8

    9

    10

    次数（单位：次）

    5

    1

    3

    1

    （1）在乙队员成绩扇形统计图中，求“8环”所在扇形的圆心角的度数；

    （2）经过整理，得到的分析数据如表：

    队员

    平均数

    中位数

    众数

    方差

    甲

    8

    7.5

    7

    c

    乙

    a

    8

    b

    1

    求表中的a、b、c的值（3）根据甲、乙两名队员的成绩情况，该射击队准备选派乙参加比赛，请你写出一条射击队选派乙的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知正方形的边长为，点从点出发，以的速度沿着折线运动，到达点时停止运动；点从点出发，也以的速度沿着折线运动，到达点时停止运动.点、分别从点、同时出发，设运动时间为.

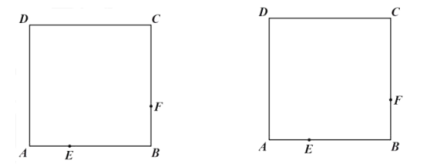
    （1）当为何值时，、两点间的距离为.

    （2）连接、交与点，

    ①在整个运动过程中，的最小值为______；

    ②当时，此时的值为______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，反比例函数的图象经过点，．

    （1）求代数式mn的值；

    （2）若二次函数的图象经过点B，求代数式的值；

    （3）若反比例函数的图象与二次函数的图象只有一个交点，且该交点在直线的下方，结合函数图象，求的取值范围．

    查看答案和解析>>

    同步练习册答案