
 如图所示,在半径为R的⊙O中,作直径AB、CD互相垂直,并把圆分成四个面积相等的扇形,在⊙O左上角的扇形OAC内再作⊙O1,使其与半径OA、OC和弧AC都相切;依此法继续作⊙O2、⊙O3…,请问所作的⊙O1的半径是
如图所示,在半径为R的⊙O中,作直径AB、CD互相垂直,并把圆分成四个面积相等的扇形,在⊙O左上角的扇形OAC内再作⊙O1,使其与半径OA、OC和弧AC都相切;依此法继续作⊙O2、⊙O3…,请问所作的⊙O1的半径是| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |

| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
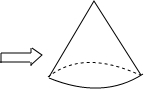 如图,现有一个半径为8cm的半圆形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),该圆锥的高为( )
如图,现有一个半径为8cm的半圆形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),该圆锥的高为( )| A、2cm | ||
B、2
| ||
| C、4cm | ||
D、4
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
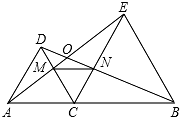 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②△ACM≌△DCN;③△ECM≌△BCN;④∠AOD=60°;⑤AC=DN.
如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②△ACM≌△DCN;③△ECM≌△BCN;④∠AOD=60°;⑤AC=DN.| A、5个 | B、4个 | C、3个 | D、2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
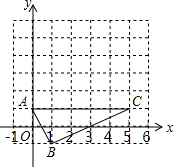 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1).
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com