

���� ��ͼ2����CD=CA=a����ACDΪ����ֱ�������Σ���AD=$\sqrt{2}$a���á�DAB=��B=22.5�㣬����DB=DA=$\sqrt{2}$a������Rt��ABC�У��������ж���ɼ����tanB=$\sqrt{2}$-1����tan22.5��=$\sqrt{2}$-1��
��ͼ3���ӳ�BA��D��ʹAD=AB����AB=AD=AC�����D=��ACD��������������������á�D=15�㣬��CH��AB��H����CH=x�����ú�30�����ߵĹ�ϵ�õ�AC=2x��AH=$\sqrt{3}$x����AD=AC=2x��DH=AD+AH=��2+$\sqrt{3}$��x��Ȼ����Rt��DCH�У��������еĶ���ɼ����tanD=2-$\sqrt{3}$����tan15��=2-$\sqrt{3}$��
��� �⣺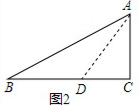 ��ͼ2����CD=CA=a����AD=$\sqrt{2}$a��
��ͼ2����CD=CA=a����AD=$\sqrt{2}$a��
�ߡ�B=22.5�㣬��ADC=45�㣬
���DAB=22.5�㣬
���DAB=��B��
��DB=DA=$\sqrt{2}$a��
��BC=BD+CD=��$\sqrt{2}$+1��a��
��Rt��ABC��tanB=$\frac{AC}{BC}$=$\frac{a}{��\sqrt{2}+1��a}$=$\sqrt{2}$-1��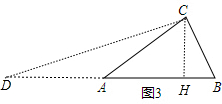
��tan22.5��=$\sqrt{2}$-1��
�ʴ�Ϊ$\sqrt{2}$-1��$\sqrt{2}$-1��
��ͼ3���ӳ�BA��D��ʹAD=AB����AB=AD=AC��
���D=��ACD��
�ߡ�CAB=��D+��ACD=30�㣬
���D=15�㣬
��CH��AB��H����CH=x����AC=2x��AH=$\sqrt{3}$x��
��AD=AC=2x��
��DH=AD+AH=��2+$\sqrt{3}$��x��
��Rt��DCH��tanD=$\frac{CH}{DH}$=$\frac{x}{��2+\sqrt{3}��x}$=2-$\sqrt{3}$��
��tan15��=2-$\sqrt{3}$��
���� ���⿼���˽�ֱ�������Σ���ֱ���������У�����֪Ԫ����δ֪Ԫ�صĹ��̾��ǽ�ֱ�������Σ��������Ĺؼ��ǹ�����22.5�Ⱥ�15�ȵ�ֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �����κ���y=ax2+bx+c��x��y�IJ��ֶ�Ӧֵ���±���
�����κ���y=ax2+bx+c��x��y�IJ��ֶ�Ӧֵ���±���| x | �� | -4 | -3 | -2 | -1 | 0 | �� |
| y | �� | -5 | 0 | 3 | 4 | 3 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��0 | B�� | 0��a��1 | C�� | 0��a��1 | D�� | a��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ı���ABCD�ڽ��ڡ�O������ABC=40�㣬���ADC�Ķ����ǣ�������
��ͼ���ı���ABCD�ڽ��ڡ�O������ABC=40�㣬���ADC�Ķ����ǣ�������| A�� | 90�� | B�� | 100�� | C�� | 120�� | D�� | 140�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 62��82��102 | B�� | 6��8��9 | C�� | 2��$\sqrt{3}$��$\sqrt{5}$ | D�� | $\sqrt{2}$��$\sqrt{3}$��$\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��4��8 | B�� | 4��4��8 | C�� | 5��6��10 | D�� | 6��7��14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com