
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
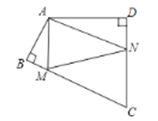
A.140°B.130°C.120°D.110°
【答案】A
【解析】
根据要使△AMN的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=70°,进而得出∠MAB+∠NAD=70°,即可得出答案.
解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
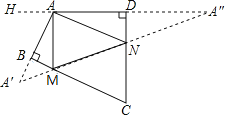
∵∠DAB=110°,
∴∠HAA′=70°,
∴∠AA′M+∠A″=∠HAA′=70°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×70°=140°,
故选A.


科目:初中数学 来源: 题型:
【题目】我们规定:若抛物线的顶点在坐标轴上,则称该抛物线为“数轴函数”例如抛物线y=x2和y=(x-1)2都是“数轴函数”.
(1)抛物线y=x2-4x+4和抛物线y=x2-6x是“数轴函数“吗?请说明理由;
(2)若抛物线y=2x2+4mx+m2+16是“数轴函数”,求该抛物线的表达式
查看答案和解析>>
科目:初中数学 来源: 题型:
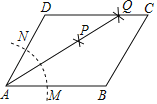
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
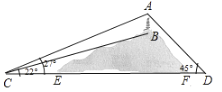
【题目】如图,山顶有一塔![]() ,塔高
,塔高![]() .计划在塔的正下方沿直线
.计划在塔的正下方沿直线![]() 开通穿山隧道
开通穿山隧道![]() .从与
.从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 、
、![]() 的仰角分别为
的仰角分别为![]() 、
、![]() ,从与
,从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 的仰角为
的仰角为![]() .求隧道
.求隧道![]() 的长度.(参考数据:
的长度.(参考数据:![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 交抛物线于点
交抛物线于点![]() .
.
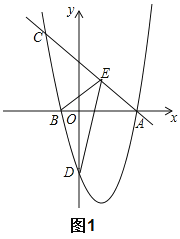
(1)求此抛物线的解析式;
(2)在线段![]() 上有一动点
上有一动点![]() ,当点
,当点![]() 在某个位置时,
在某个位置时,![]() 的面积为
的面积为![]() ,求此时
,求此时![]() 点坐标;
点坐标;
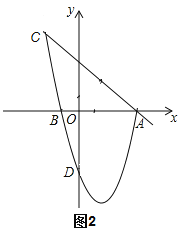
(3)如图2,当动点![]() 在直线
在直线![]() 与抛物线围成的封闭线
与抛物线围成的封闭线![]() 上运动时,是否存在以
上运动时,是否存在以![]() 为直角边的直角三角形
为直角边的直角三角形![]() ,若存在,请求出符合要求的所有
,若存在,请求出符合要求的所有![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 为
为![]() .
.
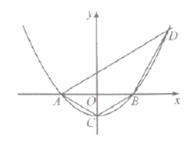
(1)求抛物线的解析式.
(2)过点![]() 作直线
作直线![]() 与抛物线在第一象限的交点为
与抛物线在第一象限的交点为![]() .当
.当![]() 时,确定直线
时,确定直线![]() 与
与![]() 的位置关系.
的位置关系.
(3)在第二象限抛物线上求一点![]() ,使
,使![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,甲、乙两家网店以同样价格销售相同的防疫用品,它们的优惠方案分别为:甲店,一次性购物中超过100元后的价格部分打七折;乙店,一次性购物中超过500元后的价格部分打五折,设商品原价为![]() 元(
元(![]() ),购物应付金额为
),购物应付金额为![]() 元.
元.
(1)求出在甲店购物时![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
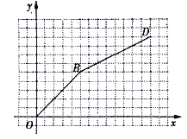
(2)在乙店购物时![]() 与
与![]() 之间的函数图像如图所示(图中线段
之间的函数图像如图所示(图中线段![]() 、射线
、射线![]() ),请在图中画出(l)中所得函数当
),请在图中画出(l)中所得函数当![]() 时的图像,并分别写出该图像与图中
时的图像,并分别写出该图像与图中![]() 、
、![]() 的交点
的交点![]() 和
和![]() 的坐标;
的坐标;
(3)根据函数图像,请直接写出新冠肺炎疫情期间选择哪家网店购物更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将三角形
将三角形![]() 折叠,得三角形
折叠,得三角形![]() .
.
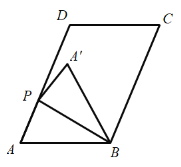
(1)当![]() 时,
时,![]() =_______度;
=_______度;
(2)如图,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;
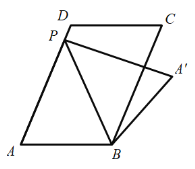
(3)当点![]() 落在平行四边形
落在平行四边形![]() 的边上时,直接写出线段
的边上时,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com