
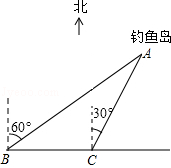
 如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行50海里与钓鱼岛A的距离最近?
如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行50海里与钓鱼岛A的距离最近? 分析 过点A作AD⊥BC于D,则垂线段AD的长度为与钓鱼岛A最近的距离,线段CD的长度即为所求.先由方位角的定义得出∠ABC=30°,∠ACD=60°,由三角形外角的性质得出∠BAC=30°,则CA=CB=100海里,然后解直角△ADC,求出CD,从而得出答案.
解答 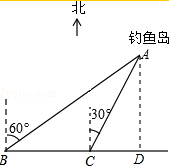 解:过点A作AD⊥BC于D,则∠ABC=30°,∠ACD=60°,
解:过点A作AD⊥BC于D,则∠ABC=30°,∠ACD=60°,
∴∠BAC=∠ACD-∠ABC=30°,
∴CA=CB.
∵CB=50×2=100(海里),
∴CA=100(海里),
在直角△ADC中,∠ACD=60°,
∴CD=$\frac{1}{2}$AC=$\frac{1}{2}$×100=50(海里).
则船继续航行50海里与钓鱼岛A的距离最近;
故答案为:50.
点评 本题考查了解直角三角形的应用-方向角问题,求三角形的边或高的问题时,一般可以转化为解直角三角形的问题,解决的方法就是作高线.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
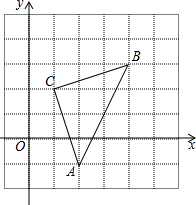 如图,在直角坐标系中△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
如图,在直角坐标系中△ABC的顶点都在网格点上,其中,C点坐标为(1,2),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
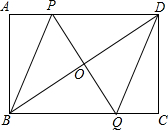 如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
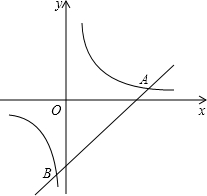 如图,已知一次函数y1=x-6与反比例函数y2=$\frac{7}{x}$的图象交于A、B两点.
如图,已知一次函数y1=x-6与反比例函数y2=$\frac{7}{x}$的图象交于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
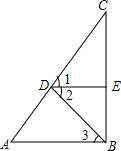 如图,∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.
如图,∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com