
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点A,反比例函数
的图象相交于点A,反比例函数![]() 的图象经过点A,反比例函数
的图象经过点A,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)直接写出![]() 时,x的取值范围;
时,x的取值范围;
(3)在x轴上是否存在点P,使△ABP为直角三角形,若存在请求出P点坐标,若不存在,请说明理由.
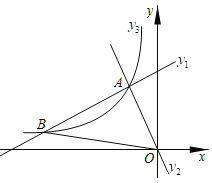
【答案】(1)y=-![]() ;(2)x<-8或-2<x<0;(3)在x轴上存在点P1(-
;(2)x<-8或-2<x<0;(3)在x轴上存在点P1(-![]() 、0)P2(0、0)使△PAB为直角三角形
、0)P2(0、0)使△PAB为直角三角形
【解析】
(1)联立一次函数![]() 和
和![]() ,解出A点坐标,代入反比例函数解析式即可求出;
,解出A点坐标,代入反比例函数解析式即可求出;
(2)联立![]() 和y=-
和y=-![]() 解出B点坐标,结合图像即可得出答案;
解出B点坐标,结合图像即可得出答案;
(3)假设在x轴上存在P(t、0)使△PAB为直角三角形,用含t的代数式表示PA2,
PB2,AB2,然后根据勾股定理分①PA2+PB2=PC2;②PA2=PB2+PC2;③PB2=PA2+AB2三种情况讨论即可.
(1)解:依题得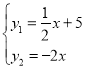
解得![]() ,即A(-2、4)
,即A(-2、4)
将A(-2、4)代入![]() 得k=-8,即反比例函数解析式为:y=-
得k=-8,即反比例函数解析式为:y=-![]() ;
;
(2)∵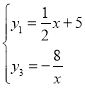
解得: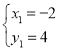 或
或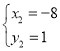 ,即B(-8、1)
,即B(-8、1)
∴结合图像可得当y1<y3时,x的取值范围是x<-8或-2<x<0;
(3)如图,假设在x轴上存在P(t、0)使△PAB为直角三角形,
∵ PA2=(t+2)2+42=t2+4t+20
PB2=(t+8)2+1=t2+16t+65
AB2=62+32=45
①PA2+PB2=PC2,即t2+4t+20+t2+16t+65=45
化简得t2+t+1=0
此时方程无解,故此种情况不成立;
②PA2=PB2+PC2 即t2+4t+20=t2+16t+65+45
解得:t=-![]() ;
;
③PB2=PA2+AB2 即t2+16t+65=45+t2+4t+20
解得:t=0;
综上所,在x轴上存在点P1(-![]() 、0),P2(0、0)使△PAB为直角三角形.
、0),P2(0、0)使△PAB为直角三角形.


科目:初中数学 来源: 题型:
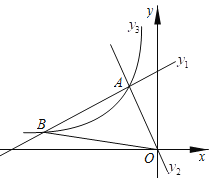
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2﹣4ac>0;②abc<0;③4a+b=0;④4a﹣2b+c>0.其中正确结论的个数是( )
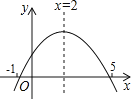
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点坐标为![]() 的抛物线
的抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴的交点在
轴的交点在![]() ,
,![]() 之间(含端点),则下列结论:①
之间(含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数
;③对于任意实数![]() ,
,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为( )
有两个不相等的实数根.其中结论正确的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(概念认识)
若以圆的直径的两个端点和圆外一点为顶点的三角形是等腰三角形,则圆外这一点称为这个圆的径等点.
(数学理解)
(1)如图①,AB是⊙O的直径,点P为⊙O外一点,连接AP交⊙O于点C,PC=AC.
求证:点P为⊙O的径等点.

(2)已知AB是⊙O的直径,点P为⊙O的径等点,连接AP交⊙O于点C,若PC=2AC.求![]() 的值.
的值.
(问题解决)
(3)如图②,已知AB是⊙O的直径.若点P为⊙O的径等点,连接AP交⊙O于点C,PC=3AC.利用直尺和圆规作出所有满足条件的点P.(保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了检测疫情期间的学习效果,某班依据学校要求进行了测试,并将成绩分成![]() 五个等级,依据相关数据绘制如下不完整统计图表如下,请解答问题:
五个等级,依据相关数据绘制如下不完整统计图表如下,请解答问题:
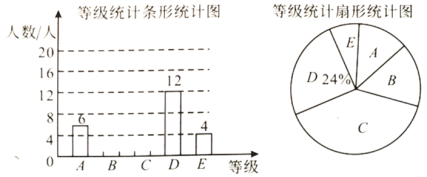
(1)该班参与测试的人数为________;
(2)![]() 等级的人数之比为
等级的人数之比为![]() ,依据数据补全统计图;
,依据数据补全统计图;
(3)扇形图中,![]() 等级人数所对应的扇形图中的圆心角为________;
等级人数所对应的扇形图中的圆心角为________;
(4)若全年级共有1400人,请估计年级部测试等级在![]() 等级以上(包括
等级以上(包括![]() 级)的学生人数.
级)的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
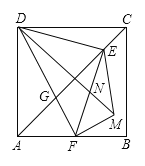
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,若点
,若点![]() 是
是![]() 的中点,则
的中点,则![]() 的周长是( )
的周长是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
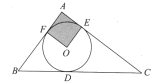
A.4B.6.25C.7.5D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庆祝建国70周年暨我爱我家·美丽菏泽群众文艺展演圆满落幕,某学习小组对文艺展演中的![]() 舞蹈《不忘初心》,
舞蹈《不忘初心》,![]() 独舞《梨园一生》,
独舞《梨园一生》,![]() 舞蹈《炫动的牡丹》,
舞蹈《炫动的牡丹》,![]() 民族歌舞组合《阿里郎+
民族歌舞组合《阿里郎+![]() 》这四个节目开展“我最喜爱的舞蹈节目”调查,随机调查了部分观众(每位观众必选且只能选这四个节目中的一个)并将得到的信息绘制了下面两幅不完整的统计图:
》这四个节目开展“我最喜爱的舞蹈节目”调查,随机调查了部分观众(每位观众必选且只能选这四个节目中的一个)并将得到的信息绘制了下面两幅不完整的统计图:
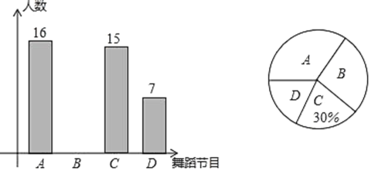
(1)本次一共调查了多少名观众?
(2)将条形统计图补充完整,并求出扇形统计图中![]() 所对应的圆心角的度数;
所对应的圆心角的度数;
(3)学习小组准备从4个节目中随机选取两个节目的录像带回学校给同学们观看,请用树状图或者列表的方法求恰好选中![]() 舞蹈《不忘初心》和
舞蹈《不忘初心》和![]() 舞蹈《炫动的牡丹》的概率.
舞蹈《炫动的牡丹》的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com