
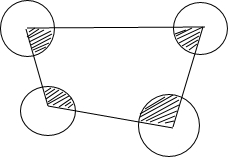
 如图所示,分别以四边形的各个顶点为圆心,半径为10作圆(这些圆互不相交).问这些圆与四边形的公共部分(即图中阴影部分)的面积是多少?为什么?
如图所示,分别以四边形的各个顶点为圆心,半径为10作圆(这些圆互不相交).问这些圆与四边形的公共部分(即图中阴影部分)的面积是多少?为什么?科目:初中数学 来源: 题型:
| A、(2x+3y)2=4x2+9y2 | ||||||||||
B、(-c+
| ||||||||||
C、(
| ||||||||||
| D、(2a+5b)2=4a2+10ab+25b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
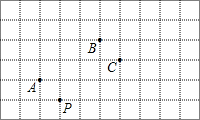 如图,在每个小方格都是正方形的网格中,一颗棋子从P点开始依次关于点A,B,C作循环对称跳动,即第一次跳到P点关于A点的对称点M处,第二次跳到M点关于B点的对称点N处,第三次跳到N点关于C点的对称点处,…,以此类推,循环往复,经过2015次跳动后,距离棋子落点最近的点是( )
如图,在每个小方格都是正方形的网格中,一颗棋子从P点开始依次关于点A,B,C作循环对称跳动,即第一次跳到P点关于A点的对称点M处,第二次跳到M点关于B点的对称点N处,第三次跳到N点关于C点的对称点处,…,以此类推,循环往复,经过2015次跳动后,距离棋子落点最近的点是( )| A、点A | B、点B | C、点C | D、点P |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com