
【题目】如图,等腰![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上不与点
上不与点![]() 、
、![]() 重合的一个动点,直线
重合的一个动点,直线![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() .当
.当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长为_______.
的长为_______.

【答案】![]() 或
或![]()
【解析】
根据勾股定理求出BC,分两种情况:①当AF=CF时,∠FAC=∠C=45°,∠AFC=90°,根据等腰直角三角形的性质得出BF=CF=![]() BC=1,根据直线
BC=1,根据直线![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,求出BD=
,求出BD=![]() BF=
BF=![]() ;②当CF=CA=
;②当CF=CA=![]() 时,BF=BC-CF=2-
时,BF=BC-CF=2-![]() ,根据直线
,根据直线![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,求出BD=
,求出BD=![]() BF=
BF=![]() .
.
∵等腰![]() 中,
中,![]() ,
,
∴BC=2,∠B=∠C=45°,
分两种情况:
①当AF=CF时,∠FAC=∠C=45°,
∴∠AFC=90°,
∴AF⊥BC,
∴BF=CF=![]() BC=1,
BC=1,
∵直线![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,
∴BD=![]() BF=
BF=![]() ;
;
②当CF=CA=![]() 时,BF=BC-CF=2-
时,BF=BC-CF=2-![]() ,
,
∵直线![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,
∴BD=![]() BF=
BF=![]() ,
,
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
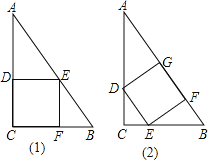
【题目】直角三角形的铁片ABC的两条直角边BC,AC的长分别为3cm和4cm,如图所示分别采用⑴,⑵两种方法,剪去一块正方形铁片,为了使剪去正方形铁片后剩下的边角料较少,试比较哪一种剪法较为合理,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B(A在B左侧)两点, 一次函数y=-x+4与坐标轴分别交于点C、D,与抛物线交于点M、N,其中点M的横坐标是
与x轴交于A、B(A在B左侧)两点, 一次函数y=-x+4与坐标轴分别交于点C、D,与抛物线交于点M、N,其中点M的横坐标是![]() .
.
(1)求出点C、D的坐标;
(2)求抛物线的表达式以及点A、B的坐标;
(3)在平面内存在动点P(P不与A,B重合),满足∠APB为直角,动点P到直线CD的距离是否有最小值,如果有,请直接写出这个最小值的结果;如果没有,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
如图1,![]() 和
和![]() 都是等腰直角三角形,其中
都是等腰直角三角形,其中![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

操作发现:如图2,保持点![]() 不动,
不动,![]() 绕点
绕点![]() 按顺时针旋转角度
按顺时针旋转角度![]() (
(![]() ),连接
),连接![]() 与
与![]() .
.

(1)猜想线段![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
拓展探究:如图3,![]() 绕点
绕点![]() 继续按顺时针旋转,当点
继续按顺时针旋转,当点![]() ,
,![]() ,
,![]() 在同一直线上时,过点
在同一直线上时,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.

(2)求![]() 的度数;
的度数;
(3)直接写出线段![]() ,
,![]() ,
,![]() 之间的的数量关系.
之间的的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
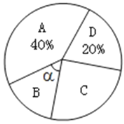
【题目】2019年10月,某市高质量通过全国文明城市测评,该成绩的取得得益于领导高度重视(A)、整改措施有效(B)、市民积极参与(C)、市民文明素质(D).某数学兴趣小组随机走访了部分市民,对这四项认可度进行调查(只选填最认可的一项),并将调查结果制作了如下两幅不完整的统计图.
(1)请补全D项的条形图;
(2)已知B、C两项条形图的高度之比为3:5.
①选B、C两项的人数各为多少个?
②求α的度数,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com