
分析 (1)根据已知得出3x2-2x=1,再整体代入所求代数式即可;
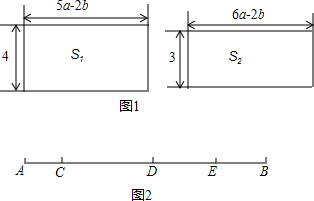
(2)列出代数式,整理成含有a-b的形式,再将a-b=2代入即可;
(3)将所有线段列出整理为含有2AB+CE=10的形式,再代入即可.
解答 解:(1)∵14x+5-21x2=-2,
∴14x-21x2=-7,
即2x-3x2=-1,
∴3x2-2x=1,
则3x2-2x+5=1+5=6;
(2)两个长方形面积的差是:S1-S2=4(5a-2b)-(6a-2b)=20a-8b-(18a-6b)=2a-2b=2(a-b),
当a-b=4时,S1-S2=2×4=8;
(3)图中线段的和为:(AC+CD+DE+EB)+(AD+DB+CE)+(AE+CE)+AB=4AB+2CE=20.
点评 本题主要考查了代数式求值,整理为已知的形式,整体代入是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=3,b=2 | B. | a=4,b=-1 | C. | a=1,b=0 | D. | a=1,b=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
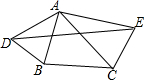 如图,△ABC中,AB=6,AC=8,分别以AB、AC为一边向外作等腰△ADB和等腰△ACE,AD=AB,AE=AC,且∠DAB=∠EAC=x,∠BAC=y(其中2x+y<180°).
如图,△ABC中,AB=6,AC=8,分别以AB、AC为一边向外作等腰△ADB和等腰△ACE,AD=AB,AE=AC,且∠DAB=∠EAC=x,∠BAC=y(其中2x+y<180°).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
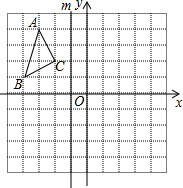 如图所示的正方形网格中,每个小正方形的边长为1,△ABC的三个顶点都在格点上.
如图所示的正方形网格中,每个小正方形的边长为1,△ABC的三个顶点都在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com