
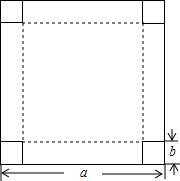
 在一块边长为a厘米的正方形纸板四角,各剪去一个边长为b(b<
在一块边长为a厘米的正方形纸板四角,各剪去一个边长为b(b<| a |
| 2 |
| a |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
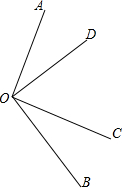 如图所示,∠AOC和∠BOD都是直角.
如图所示,∠AOC和∠BOD都是直角.查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)这圆锥侧面展开的圆心角为n°,母线长为R,底面半径为r,填表:
(1)这圆锥侧面展开的圆心角为n°,母线长为R,底面半径为r,填表:| n | 60° | 72° | 90° | 120° |
| R与r之间的函数解析式 |
查看答案和解析>>
科目:初中数学 来源: 题型:
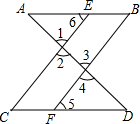 如图,已知∠1=∠4,∠B=∠C,判断∠A与∠D的大小关系,并说明理由.小明同学给出了如下解答.
如图,已知∠1=∠4,∠B=∠C,判断∠A与∠D的大小关系,并说明理由.小明同学给出了如下解答.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在三角形ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,已知∠A=60°,∠DFB=75°,∠ADE=45°
如图,在三角形ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,已知∠A=60°,∠DFB=75°,∠ADE=45°查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,是一个可以转动的圆盘,指针固定不动,六个扇形的圆心角相等.转动转盘等他停下后指针指向几,就按顺时针走几格,得到一个数字.分别求得到数字为偶数和奇数的概率.
如图,是一个可以转动的圆盘,指针固定不动,六个扇形的圆心角相等.转动转盘等他停下后指针指向几,就按顺时针走几格,得到一个数字.分别求得到数字为偶数和奇数的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com