
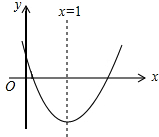
 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0;⑤3b<2c,其中正确的个数( )
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0;⑤3b<2c,其中正确的个数( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 由抛物线开口向上,得到a>0,再由对称轴在y轴右侧,得到a与b异号,可得出b<0,又抛物线与y轴正半轴相交,得到c>0,可得出abc<0,选项①错误;最后由对称轴为直线x=1,利用对称轴公式得到2a+b=0,选项②正确;由抛物线与x轴有2个交点,得到根的判别式b2-4ac大于0,故③错误;由x=2时对应的函数值>0,将x=2代入抛物线解析式可得出4a+2b+c大于0,得到选项④正确;最后由对称轴为直线x=1,利用对称轴公式得到a=-$\frac{1}{2}$b,由x=-1时对应的函数值小于0,将x=-1代入抛物线解析式可得出y=a-b+c<0,即可得出3b<2c,即可得到⑤正确.
解答 解:∵抛物线的开口向上,∴a>0,
∵-$\frac{b}{2a}$>0,∴b<0,
∵抛物线与y轴交于正半轴,∴c>0,
∴abc<0,①错误;
∵对称轴为直线x=1,∴-$\frac{b}{2a}$=1,即2a+b=0,②正确,
∵抛物线与x轴有2个交点,∴b2-4ac>0,③错误;
∵对称轴为直线x=1,
∴x=2时,y>0,∴4a+2b+c>0,④正确;
∵2a+b=0,∴a=-$\frac{1}{2}$b,
∵x=-1时,y=a-b+c>0,
∴-$\frac{1}{2}$b-b+c>0,
∴3b<2c,故⑤正确
则其中正确的有②④⑤.
故选B.
点评 本题考查了二次函数图象与系数的关系,二次函数y=ax2+bx+c(a≠0),a的符号由抛物线开口方向决定;b的符号由对称轴的位置及a的符号决定;c的符号由抛物线与y轴交点的位置决定;抛物线与x轴的交点个数,决定了b2-4ac的符号,此外还要注意x=1,-1,2及-2对应函数值的正负来判断其式子的正确与否.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 已知:如图,在?ABCD中,点E在BC边上,连接AE,O为AE中点,连接BO并延长交AD于F.
已知:如图,在?ABCD中,点E在BC边上,连接AE,O为AE中点,连接BO并延长交AD于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处径直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )
如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处径直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )| A. | 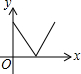 | B. | 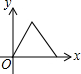 | C. | 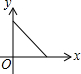 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
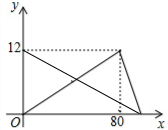 完全相同的甲、乙两个水槽,分别有一个进水管和若干个出水管,甲槽有12升水,由于工作人员马虎,他关闭进水管和出水管时,有一个出水管未关,水以每分钟0.12升的速度滴下,乙槽原来没有水,同时开放进水管和一个出水管一段时间后,关闭进水管,又打开a个出水管,存水量y(升)与时x(分)之间的函数图象如图所示,请结合图象回答问题:
完全相同的甲、乙两个水槽,分别有一个进水管和若干个出水管,甲槽有12升水,由于工作人员马虎,他关闭进水管和出水管时,有一个出水管未关,水以每分钟0.12升的速度滴下,乙槽原来没有水,同时开放进水管和一个出水管一段时间后,关闭进水管,又打开a个出水管,存水量y(升)与时x(分)之间的函数图象如图所示,请结合图象回答问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com