
【题目】写出下列命题的已知、求证,并完成证明过程.
命题:如果一个三角形的两条边相等,那么两条边所对的角也相等(简称:“等边对等角”.)
已知:( ).
求证:( ).
证明:
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】某物流公司承接A,B两种货物运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨;该物流公司6月承接的A种货物和B种数量与5月份相同,6月份共收取运费13000元.
(1)该物流公司月运输两种货物各多少吨?
(2)该物流公司预计7月份运输这两种货物330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收到多少运输费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,学校对“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题密切关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对这一问题的看法人数统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 40 | 60 | m |

(1)求n的值;
(2)统计表中的m=;
(3)估计该校1800名学生中认为“影响很大”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米.
(1)按如图所示建立平面直角坐标系,求表示该抛物线的函数表达式;
(2)一辆货运卡车高为4m,宽为2m,如果该隧道内设双向车道,那么这辆货车能否安全通过?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP,BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是 . 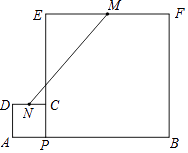
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com