
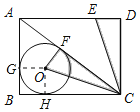
【题目】如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,点E是边AD上一点,连结CE,将△CDE绕点C旋转,当CD落到对角线AC上时,点E恰与圆心O重合,已知AE=6,则下列结论不正确的是( )

A. BC+DE=ACB. ⊙O 的半径是2
C. ∠ACB=2∠DCED. AE=CE
【答案】D
【解析】
⊙O是△ABC的内切圆,设半径为r,切点分别为F、G、H,连接OG、OH,则四边形BGOH是正方形,得出OG=OG=BG=BH=r,由旋转的性质得:OF=DE=r,CF=CD,∠FCO=∠DCE,得出∠ACB=2∠DCE,在Rt△ABC中,由勾股定理得出方程,解方程得出r=2,BC=8,AC=10,选项A、B、C正确;由勾股定理得:CE=![]() ,选项D不正确.
,选项D不正确.
解:⊙O是△ABC的内切圆,设半径为r,切点分别为F、G、H,连接OG、OH,如图:
则四边形BGOH是正方形,
∴OG=OG=BG=BH=r,
由旋转的性质得:OF=DE=r,CF=CD,∠FCO=∠DCE,
∴∠ACB=2∠DCE,
∵BC=AD,
∴AB=CD=CF=AE=6,
由切线长定理得:CH=CF=CD=6,∠ACO=∠BCO,AF=AG=6﹣r,
∴AC=AF+CF=12﹣r,
在Rt△ABC中,由勾股定理得:62+(6+r)2=(12﹣r)2,
解得:r=2,∴BC=8,AC=10,
∴BC+DE=AC,⊙O 的半径是2,
所以选项A、B、C正确;
由勾股定理得:![]() ,选项D不正确;
,选项D不正确;
故选:D.


科目:初中数学 来源: 题型:
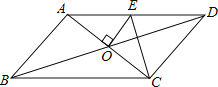
【题目】如图,ABCD的周长为22m,对角线AC、BD交于点O,过点O与AC垂直的直线交边AD于点E,则△CDE的周长为( )
A. 8cmB. 9cmC. 10cmD. 11cm
查看答案和解析>>
科目:初中数学 来源: 题型:
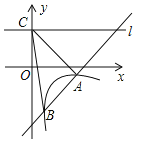
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于A(2,-1)、B(
(x>0)的图象交于A(2,-1)、B(![]() ,n)两点,点C的坐标为(0,2),过点C的直线l与x轴平行.
,n)两点,点C的坐标为(0,2),过点C的直线l与x轴平行.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,等边△AOB的边长为10,点C在边OA上,点D在边AB上,且OC=3BD.反比例函数y=![]() (k≠0)的图象恰好经过C、D两点,则k的值为_____.
(k≠0)的图象恰好经过C、D两点,则k的值为_____.
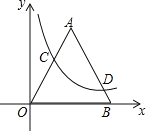
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是一款手机支架,忽略支管的粗细,得到它的简化结构图如图(2)所示.已知支架底部支架CD平行于水平面,EF⊥OE,GF⊥EF,支架可绕点O旋转,OE=20cm,EF=20![]() cm.如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
cm.如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
(1)求FG的长度(结果精确到0.1);
(2)将支架由图(3)转到图(4)的位置,若此时F、O两点所在的直线恰好于CD垂直,点F的运动路线的长度称为点F的路径长,求点F的路径长.
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数y=![]() (x>0)的图象G经过点A(4,1),直线l:y=
(x>0)的图象G经过点A(4,1),直线l:y=![]() +b与图象G交于点B,与y轴交于点C.
+b与图象G交于点B,与y轴交于点C.
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,B之间的部分与线段OA,OC,BC围成的区域(不含边界)为w.
①当b=﹣1时,直接写出区域W内的整点个数;
②若区域W内恰有4个整点,结合函数图象,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数 y=![]() 的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
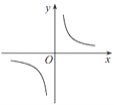
A.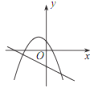 B.
B.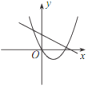 C.
C.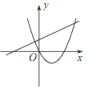 D.
D.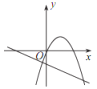
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若一次函数y=ax+b和反比例函数y=-![]() 满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
(1)判断y=x+b和y=-![]() 是否存在“等差”函数?若存在,写出它们的“等差”函数;
是否存在“等差”函数?若存在,写出它们的“等差”函数;
(2)若y=5x+b和y=-![]() 存在“等差”函数,且“等差”函数的图象与y=-
存在“等差”函数,且“等差”函数的图象与y=-![]() 的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
(3)若一次函数y=ax+b和反比例函数y=-![]() (其中a>0,c>0,a=
(其中a>0,c>0,a=![]() b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com