
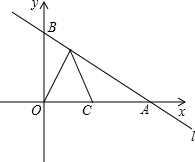
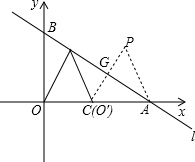
 如图所示,在平面直角坐标系中,过B的直线l:y=kx+1与x轴交于A点,且∠BAO=30°.
如图所示,在平面直角坐标系中,过B的直线l:y=kx+1与x轴交于A点,且∠BAO=30°.| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
3
| ||
| 16 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
| a-b |
| a+b |
| A、大于0 | B、小于0 |
| C、等于0 | D、不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=4km,BC=2km,CD=3km,DE=3km,EF=1km,他们全部乘出租车上班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算),每辆车能容纳3人.
在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=4km,BC=2km,CD=3km,DE=3km,EF=1km,他们全部乘出租车上班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算),每辆车能容纳3人.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,∠BAC=60°,在△ABC的内部取一点O,连接OA,OB,OC,恰有OA=OC,∠OBA=20°,∠OCA=40°.①∠BOA=140°;②△OAB是等腰三角形;③∠OBC=30°;④△OBC是等腰三角形;⑤△ABC是等边三角形,则以上说法中正确的是( )
如图,在△ABC中,∠BAC=60°,在△ABC的内部取一点O,连接OA,OB,OC,恰有OA=OC,∠OBA=20°,∠OCA=40°.①∠BOA=140°;②△OAB是等腰三角形;③∠OBC=30°;④△OBC是等腰三角形;⑤△ABC是等边三角形,则以上说法中正确的是( )| A、①②③④⑤ | B、①②③④ |
| C、①②③⑤ | D、①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com