
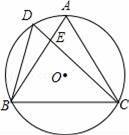
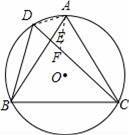
如图,D是正△ABC的外接圆⊙O上弧AB上一点,给出下列结论:①∠BDC=∠ADC=60°;②AE•BE=CE•ED;③CA2=CE•CD;④CD=BD+AD.其中正确的个数是( )

A.4 B.3 C.2 D.1
A【考点】相似三角形的判定与性质;等边三角形的性质;圆周角定理.
【分析】连接AD,根据等边三角形的性质得到∠BAC=∠ABC=60°,由圆周角定理得到∠BDC=∠BAC=60°,∠ADC=∠ABC=60°,于是得到∠BDC=∠ADC=60°,故①正确;根据圆周角定理得到∠D=∠A,∠ABD=∠ACD,推出△BDE∽△ACE,根据相似三角形的性质即可得到AE•BE=CE•ED;故②正确;由于∠ADC=∠EAC=60°,∠ACE=∠ACD,得到△ACD∽△ACE,根据相似三角形的性质得到CA2=CE•CD;故③正确;在CD上截取CF=BD,通过△ABD≌△ACF,得到AD=AF,推出△ADF是等边三角形,得到DF=AD,等量代换即可得到结论.
【解答】解:连接AD,∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,
∴∠BDC=∠BAC=60°,∠ADC=∠ABC=60°,
∴∠BDC=∠ADC=60°,故①正确;
∵∠D=∠A,∠ABD=∠ACD,
∴△BDE∽△ACE,
∴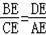
 ,
,
∴AE•BE=CE•ED;故②正确;
∵∠ADC=∠EAC=60°,∠ACE=∠ACD,
∴△ACD∽△ACE,
∴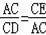
 ,
,
∴CA2=CE•CD;故③正确;
在CD上截取CF=BD,
在△ABD与△ACF中,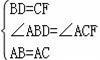
 ,
,
∴△ABD≌△ACF,
∴AD=AF,
∵∠ADC=60°,
∴△ADF是等边三角形,
∴DF=AD,
∵CD=CF+DF,
∴CD=BD+AD.故④正确.
故选A.

【点评】此题考查了圆周角定理,全等三角形的判定和性质,等边三角形的性质,相似三角形的判定与性质,熟练掌握定理及性质是解本题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
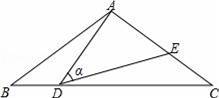
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=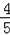
 ,则线段CE的最大值为 .
,则线段CE的最大值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下列材料,然后回答问题:
在进行二次根式运算时,我们有时会碰上如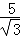 、
、 这样的式子,其实我们还可以将其进一步化简:
这样的式子,其实我们还可以将其进一步化简: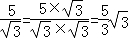 ;
;
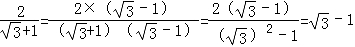 .以上这种化简过程叫做分母有理化.
.以上这种化简过程叫做分母有理化.
 还可以用以下方法化简:
还可以用以下方法化简: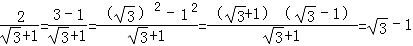 .
.
(1)请用其中一种方法化简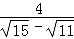 ;
;
(2)化简: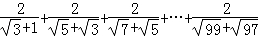 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线
 (x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(1)分别求出直线AB及双曲线的解析式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时,y1>y2?


查看答案和解析>>
科目:初中数学 来源: 题型:
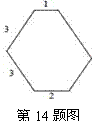
一个六边形的六个内角都是120o(如图),连续四条边的长依次为 1,3,3,2,
则这个六边形 的周长是( )
A. 13 B. 14 C. 15 
 D. 16
D. 16
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在长为8cm、宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )

A.2cm2 B.4cm2 C.8cm2 D.16cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com