练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，某会展中心在一次会展期间准备在楼梯上铺地毯，已知楼梯的高BC为5m，斜面AC为13m，每一级楼梯宽AD为2m，地毯的价格为每平方米20元，铺完这个楼梯至少需要多少元钱？
    考点：勾股定理的应用
    专题：
    分析：先根据勾股定理求出AB的长，再求出地毯的面积，进而可得出结论．
    解答：解：∵AC=13m，BC=5m，
    ∴AB=
    		132-52
    =12m．
    ∴地毯总长为12+5=17（m），
    ∴地毯的总面积为17×2=34（平方米）．
    ∵毯的价格为每平方米20元，
    ∴铺完这个楼道至少需要34×20=680（元）．
    答：铺完这个楼梯至少需要680元钱．
    点评：本题考查的是勾股定理的应用，熟知勾股定理是解答此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，若AB为⊙O的直径，CD是⊙O的弦，∠ABD=65°，则∠BCD的度数为（　　）
    A、25°B、45°
    C、55°D、75°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，AD是∠BAC的平分线，AB=8cm，AC=6cm，则S△ABD：S△ACD=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，∠C=90°，AC=BC，AD是∠A的平分线，交CB于点D．
    （1）求证：AB=AC+CD；
    （2）若AC=3，求BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，在长为a厘米、宽为
    3
    5
    a厘米的长方形纸板的四个角上各截去一个边长为b厘米的小正方形（b＜
    3
    10
    a），沿虚线折起，得到一个有底无盖的纸盒．
    （1）要将纸盒外部表面贴上彩纸，用代数式表示至少需要多大面积的彩纸；
    （2）当a=31，b=4.8时，求所需彩纸的面积．（精确到1平方厘米）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

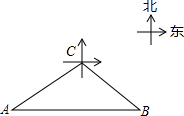    已知一艘轮船从港口A出发以80km∕h的速度向正东方向航行，30min后到港口B，又从港口B以同样的速度15min后航行到港口C，此时在C处测得港口A位于港口C的南偏西63.4°方向上，求该艘轮船以80km∕h的速度返回到港口A所需的时间．（精确到0.01h，参考数据：cos63.4°≈0.45，sin26.6°≈0.45，cos26.6°≈0.89，tan26.6°≈0.50，
    		2
    ≈1.41，
    		5
    ≈2.24）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知：BD=CE=AF，DE=DF=EF，△DEF为正三角形．求证：△ABC为正三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，点A的坐标为（2，1）．
    （1）求OA的长．
    （2）点P为x轴正半轴上的一点，且△AOP是等腰三角形，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知∠A=60°，∠B=∠D=90°，AB=2，CD=1，求BC和AD的长．

    查看答案和解析>>

    同步练习册答案