
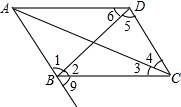
 如图,若∠2=∠6,则
如图,若∠2=∠6,则

科目:初中数学 来源: 题型:
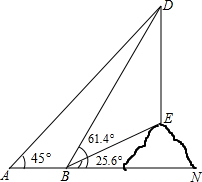 如图,课外数学活动小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直,他们在A处测塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,塔底E的仰角∠EBN=25.6°,现在请你帮助课外活动小组算一算塔高DE大约是多少米?(结果精确到个位)(参考数据:sin25.6°≈0.4,cos25.6°≈0.9,tan25.6°≈0.5,sin61.4°≈0.9,cos61.4°≈0.5,tan61.4°≈1.8)
如图,课外数学活动小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直,他们在A处测塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,塔底E的仰角∠EBN=25.6°,现在请你帮助课外活动小组算一算塔高DE大约是多少米?(结果精确到个位)(参考数据:sin25.6°≈0.4,cos25.6°≈0.9,tan25.6°≈0.5,sin61.4°≈0.9,cos61.4°≈0.5,tan61.4°≈1.8)查看答案和解析>>
科目:初中数学 来源: 题型:
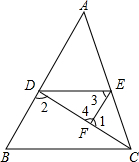 填空:
填空:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com