
关于x的一元二次方程(a-6)x2-8x+9=0有实根.
(1)求a的最大整数值;
(2)当a取最大整数值时,①求出该方程的根;②求2x2-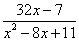 的值.
的值.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
已知关于x的一元二次方程x2-2x-a=0.
(1)如果此方程有两个不相等的实数根,求a的取值范围;
(2)如果此方程的两个实数根为x1,x2,且满足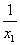 +
+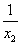 =-
=-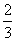 ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
函数的有关概念
| 自变量与函数 | 一般地,在某个变化过程中,如果有两个变量x和y,如果对于x的每一个值,y都有 |
| 函数的表示方法 | 列表法、图象法、解析法 |
| 函数自变量的取值范围 | ①函数解析式是整式,自变量取值是 ②函数解析式是分式,自变量取值使得 ③函数解析式是偶次根式,自变量要使得 ④来源于实际问题的函数,自变量要使得实际问题有意义、式子有意义. |
| 函数的图象 | 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知如图,一天上午6点钟,言老师从学校出发,乘车上市里开会,8点准时到会场,中午12点钟回到学校,他这一段时间内的行程s(km)(即离开学校的距离)与时间(时)的关系可用图中的折线表示,根据图中提供的有关信息,解答下列问题:
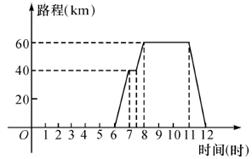
(1)开会地点离学校多远?
(2)请你用一段简短的话,对言老师从上午6点到中午12点的活动情况进行描述.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知,一次函数y=kx+3的图象经过点A(1,4).
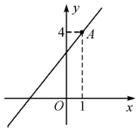
(1)求这个一次函数的解析式;
(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图象上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com