
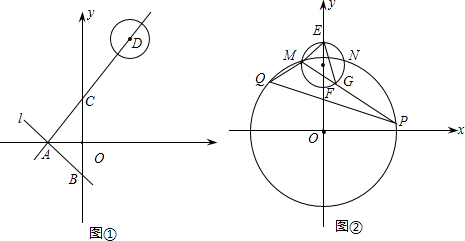
分析 (1)要求点C的坐标,只需求OC的长,只需解直角三角形AOC就可解决问题;
(2)当⊙D第一次与y轴相切于点T时,如图①,要求直线AB平移的速度,只需求出平移的距离和时间,只需解直角三角形ASA′就可求出平移的距离AA′,由于直线AB平移的时间与⊙D平移的时间相同,且⊙D平移的速度已知,只需求出⊙D平移的距离DD′即可;
(3)连接QO并延长,交⊙O于点R,连接PR、FG,如图②,根据圆内接四边形对角互补和平角的定义可得∠EMG=∠QSP=180°-∠QMP,根据圆周角定理可得∠EFG=∠EMG,从而可得∠EFG=∠QSP,根据等角的余角相等可得∠FEG=∠OQP,问题得以解决.
解答 解:(1)∵∠OAB=30°,∠BAC=90°,∴∠OAC=60°.
∵A($-2\sqrt{3}$,0),∴OA=2$\sqrt{3}$.
∵∠AOC=90°,
∴OC=OA•tan∠OAC=2$\sqrt{3}×\sqrt{3}$=6,∠ACO=30°,
∴点C的坐标为(0,6);
(2)当⊙D第一次与y轴相切于点T时,直线l平移后的直线A′B′与⊙D′相切于点S,如图①,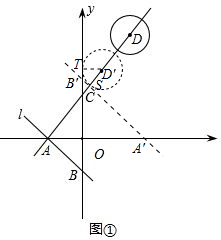
则有∠D′SA′=90°,∠D′TC=90°,D′T=2.
在Rt△D′TC中,
∵∠TCD′=∠ACO=30°,D′T=2,
∴tan30°=$\frac{2}{TC}$=$\frac{\sqrt{3}}{3}$,
∴TC=2$\sqrt{3}$,D′C=4.
同理可得DC=8,AC=4$\sqrt{3}$,
∴DD′=DC-D′C=8-4=4,
AS=D′A-D′S=D′C+AC-D′S=4+4$\sqrt{3}$-2=4$\sqrt{3}$+2.
在Rt△ASA′中,
cos60°=$\frac{AS}{AA′}$=$\frac{1}{2}$,
∴AA′=2AS=8$\sqrt{3}$+4.
∵t=$\frac{DD′}{1}$=4,
∴V=$\frac{AA′}{t}$=$\frac{8\sqrt{3}+4}{4}$=2$\sqrt{3}$+1,
∴直线l的平移速度为每秒(2$\sqrt{3}$+1)个单位长度;
(3)$\frac{∠FEG}{∠OQP}$的值不会变化.
连接QO并延长,交⊙O于点R,连接PR、FG,如图②.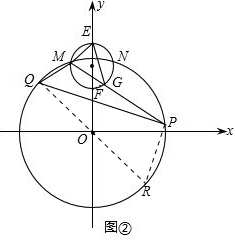
∵∠QMP+∠QRP=180°,∠EMG+∠QMP=180°,
∴∠EMP=∠QRP.
∵∠EMG=∠EFG,
∴∠EFG=∠QRP.
∵EF是⊙D的直径,QR是⊙O的直径,
∴∠EGF=90°,∠QPR=90°,
∴∠FEG+∠EFG=90°,∠OQP+∠QRP=90°,
∴∠FEG=∠OQP,
∴$\frac{∠FEG}{∠OQP}$=1(定值).
点评 本题主要考查了三角函数、运用待定系数法求直线的解析式、直线上点的坐标特征、圆的切线的性质、圆周角定理、圆内接四边形的对角互补、同角的补角相等、等角的余角相等、平角的定义等知识,综合性比较强,有一定的难度,证到∠EFG=∠EMG=∠QSP是解决第(3)小题的关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
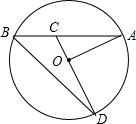 如图,已知AB是⊙O的弦,OA=4,∠A=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接BD.
如图,已知AB是⊙O的弦,OA=4,∠A=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com