
 如图,小明在高度为10m的楼顶A处,测得在同一水平面上的灯杆顶端C处的仰角为45°,灯杆底部D处的俯角为30°,求灯杆CD的高度.(结果精确到0.1m,$\sqrt{3}$取1.732)
如图,小明在高度为10m的楼顶A处,测得在同一水平面上的灯杆顶端C处的仰角为45°,灯杆底部D处的俯角为30°,求灯杆CD的高度.(结果精确到0.1m,$\sqrt{3}$取1.732) 分析 首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造关系式求解.
解答 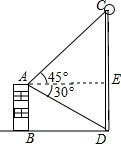 解:如图,过点A作AE⊥CD于点E,
解:如图,过点A作AE⊥CD于点E,
根据题意,∠CAE=45°,∠DAE=30°.
∵AB⊥BD,CD⊥BD,
∴四边形ABDE为矩形.
∴DE=AB=10.
在Rt△ADE中,cot∠DAE=$\frac{AE}{DE}$,
∴AE=DE•cot30°=10×$\sqrt{3}$=10$\sqrt{3}$.
在Rt△ACE中,由∠CAE=45°,
得CE=AE=10$\sqrt{3}$.
∴CD=CE+DE=10($\sqrt{3}$+1)≈27.3.
答:乙楼CD的高度约为27.3m.
点评 本题考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图所示,有一“工”字形的机器零件,它是轴对称图形,图中所有的角都是直角,图中数据单位:cm,那么A.B两点之间的距离为( )
如图所示,有一“工”字形的机器零件,它是轴对称图形,图中所有的角都是直角,图中数据单位:cm,那么A.B两点之间的距离为( )| A. | 8cm | B. | 8$\sqrt{2}$cm | C. | 16cm | D. | 16$\sqrt{2}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
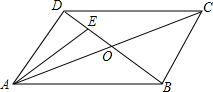 如图,在?ABCD中,对角线AC,BD相交于点O,AC=2AD,点E是OD的中点,连接AE.
如图,在?ABCD中,对角线AC,BD相交于点O,AC=2AD,点E是OD的中点,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
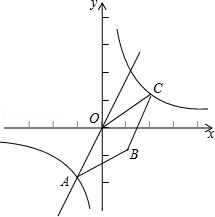 如图,已知正比例函数y=2x和反比例函数y=$\frac{k}{x}$的图象交于点A(m,-2)
如图,已知正比例函数y=2x和反比例函数y=$\frac{k}{x}$的图象交于点A(m,-2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com