
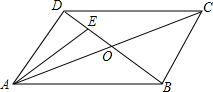
 如图,在?ABCD中,对角线AC,BD相交于点O,AC=2AD,点E是OD的中点,连接AE.
如图,在?ABCD中,对角线AC,BD相交于点O,AC=2AD,点E是OD的中点,连接AE.分析 (1)由平行四边形的性质得出AC=2OA,再证明OA=AD,由E为OD的中点,由等腰三角形的三线合一性质即可证出AE⊥BD;
(2)由已知条件得出OA、OE的长,由勾股定理求出AE,求出?ABCD的面积=2S△ABD=32$\sqrt{2}$,得出△ABD的面积=16$\sqrt{2}$,设AB,CD两条平行线间的距离为x,由勾股定理求出AB,在由△ABD的面积求出x即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AC=2OA,
∵AC=2AD,
∴OA=AD,
又∵E为OD的中点,
∴AE⊥BD;
(2)解:∵BD=8,
∴OE=2,BE=6,
∵AC=12,
∴AO=6,
∴AE=$\sqrt{A{O}^{2}-O{E}^{2}}$=$\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$,
∴?ABCD的面积=2S△ABD=2×$\frac{1}{2}$×BD•AE=8×4$\sqrt{2}$=32$\sqrt{2}$,
∴△ABD的面积=16$\sqrt{2}$,
设AB,CD两条平行线间的距离为x,
∵AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{(4\sqrt{2})^{2}+{6}^{2}}$=2$\sqrt{17}$,
则$\frac{1}{2}$x•AB=16$\sqrt{2}$,
即$\sqrt{17}$x=16$\sqrt{2}$,
∴x=$\frac{16}{17}$$\sqrt{34}$,即AB,CD两条平行线间的距离为$\frac{16}{17}$$\sqrt{34}$.
点评 本题考查了平行四边形的性质、等腰三角形的性质、勾股定理、三角形面积的计算等知识;由等腰三角形的三线合一性质得出AE⊥BD,并运用勾股定理和计算△ABD的面积使问题(2)得到解决.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:解答题
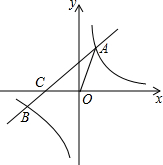 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,3),点B的坐标为(-6,n).
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,3),点B的坐标为(-6,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:m、n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图象经过点A(-m,0)、B(0,n).
已知:m、n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图象经过点A(-m,0)、B(0,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明在高度为10m的楼顶A处,测得在同一水平面上的灯杆顶端C处的仰角为45°,灯杆底部D处的俯角为30°,求灯杆CD的高度.(结果精确到0.1m,$\sqrt{3}$取1.732)
如图,小明在高度为10m的楼顶A处,测得在同一水平面上的灯杆顶端C处的仰角为45°,灯杆底部D处的俯角为30°,求灯杆CD的高度.(结果精确到0.1m,$\sqrt{3}$取1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com