练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．已知$\frac{a}{x}$+$\frac{bx+c}{{x}^{2}+4}=\frac{4}{{x（x}^{2}+4）}$，求a，b，c的值．

    分析 根据通分，同分母分式加减运算，可得相等的分式，根据相等的多项式的项相同，可得

    解答 解：通分，得
    $\frac{a{x}^{2}+4a+b{x}^{2}+cx}{x（{x}^{2}+4）}$=$\frac{4}{x（{x}^{2}+4）}$．
    由相等的分式的分子相等，得
    （a+b）x2+cx+4a=4．
    由相等的多项式的项相同，得
    $\left\{\begin{array}{l}{a+b=0}\\{c=0}\\{4a=4}\end{array}\right.$，
    解得$\left\{\begin{array}{l}{a=1}\\{b=-1}\\{c=0}\end{array}\right.$．

    点评 本题考查了分式的加减，利用通分，同分母分式加减运算得出相等的分式是解题关键，注意相等的多项式的项相同．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．分解因式：
    （1）x3-x；
    （2）x（x-y）+y（y-x）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，在一个五边形的边AB上有一点O，将O与五边形的顶点C、D、E相连，若∠COB=36°，∠DOE=54°，OC、OE分别平分∠DOB，∠AOD．
    （1）求∠EOC的度数；
    （2）写出∠COD的余角和∠AOE的补角；
    （3）分别求出∠COD的余角和∠AOE的补角的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图是一个几何体的三视图，试画出该几何体的立体图形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，正方形ABCD中，过D作DE∥AC，∠ACE=30°，CE交AD于点F，求证：AE=AF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．认真阅读下列解答过程：
    比较2-$\sqrt{3}$与$\sqrt{3}$-$\sqrt{2}$的大小．
    解：∵2-$\sqrt{3}$=（2-$\sqrt{3}$）•$\frac{2+\sqrt{3}}{2+\sqrt{3}}$=$\frac{1}{2+\sqrt{3}}$，
    $\sqrt{3}$-$\sqrt{2}$=（$\sqrt{3}$-$\sqrt{2}$）•$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}$=$\frac{1}{\sqrt{3}+\sqrt{2}}$，
    又2+$\sqrt{3}$＞$\sqrt{3}$$+\sqrt{2}$＞0，∴$\frac{1}{2+\sqrt{3}}$＜$\frac{1}{\sqrt{3}+\sqrt{2}}$，
    即2-$\sqrt{3}$＜$\sqrt{3}$-$\sqrt{2}$．
    请仿照上述方法比较$\sqrt{6}$-$\sqrt{5}$与$\sqrt{5}$-2的大小关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．若5+$\sqrt{11}$的小数部分为a，5-$\sqrt{11}$的小数部分为b，求a+b．
    解：因为3＜$\sqrt{11}$＜4，所以5+$\sqrt{11}$的整数部分为8，5-$\sqrt{11}$的整数部分为1．则5+$\sqrt{11}$的小数部分a=5+$\sqrt{11}$-8=$\sqrt{11}$-3，5-$\sqrt{11}$的小数部分b=5-$\sqrt{11}$-1=4-$\sqrt{11}$，所以a+b=$\sqrt{11}$-3+4-$\sqrt{11}$=1．
    阅读后，请解答下列问题：
    若6+$\sqrt{10}$的整数部分为a，小数部分为b，求2a-（$\sqrt{10}$+3）b+2015的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

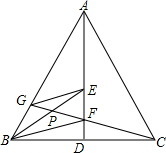    5．如图，AD是等腰△ABC底边上的高，E、F为AD上两点，且∠ABE=∠EBF=∠FBC，连接CF并延长交AB于点G，求证：
    （1）△GBF是等腰三角形；
    （2）GE∥BF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．当x=-$\frac{1}{2}$时，分式$\frac{1+2x}{x-2}$的值为0．

    查看答案和解析>>

    同步练习册答案