
分析 利用完全平方数得到3<$\sqrt{10}$<16,则可判断6+$\sqrt{10}$的整数部分为9,所以6+$\sqrt{10}$的小数部分为$\sqrt{10}$-3,即a=9,b=$\sqrt{10}$-3,然后把a、b的值代入2a-($\sqrt{10}$+3)b+2015中利用平方差公式计算.
解答 解:因为3<$\sqrt{10}$<16,所以6+$\sqrt{10}$的整数部分为9,6+$\sqrt{10}$的小数部分为6+$\sqrt{10}$-9=$\sqrt{10}$-3,
即a=9,b=$\sqrt{10}$-3,
所以2a-($\sqrt{10}$+3)b+2015=2×9-($\sqrt{10}$+3)($\sqrt{10}$-3)+2015
=18-(10-9)+2015
=2032.
点评 本题考查了无理数的估算:解题关键是确定无理数的整数部分即可解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O直径,切线CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,
如图,AB是⊙O直径,切线CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
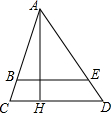 如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.
如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com