
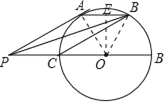
【题目】如图,过半径为2的⊙O外一点P,作⊙O的切线PA,切点为A,连接PO,交⊙O于点C,过点A作⊙O的弦AB,使AB∥PO,连接PB、BC.
(1)当点C是PO的中点时,
①求证:四边形PABC是平行四边形;
②求△PAB的面积.
(2)当AB=2![]() 时,请直接写出PC的长度.
时,请直接写出PC的长度.

【答案】(1)①见解析;②S△PAB=![]() ;(2)2
;(2)2![]() ﹣2.
﹣2.
【解析】
(1)①连接OA、OB, 由切线的性质可得OA⊥PA,根据已知条件易得OA=![]() PO,在Rt△OAP中,求得∠POA=60°,根据平行线的性质可得∠BAO=∠POA=60°,即可得△OAB是等边三角形,所以AB=OA,即AB=PC,根据一组对边平行且相等的四边形为平行四边形即可判定四边形PABC是平行四边形;②过点O作OE⊥AB,垂足为E,根据等边三角形的性质及锐角三角函数求得OA=2,OE=
PO,在Rt△OAP中,求得∠POA=60°,根据平行线的性质可得∠BAO=∠POA=60°,即可得△OAB是等边三角形,所以AB=OA,即AB=PC,根据一组对边平行且相等的四边形为平行四边形即可判定四边形PABC是平行四边形;②过点O作OE⊥AB,垂足为E,根据等边三角形的性质及锐角三角函数求得OA=2,OE=![]() ,即可求得S△OAB=
,即可求得S△OAB=![]() ABOE=
ABOE=![]() ,根据同底等高的两个三角形的面积相等即可得S△PAB=S△OAB=
,根据同底等高的两个三角形的面积相等即可得S△PAB=S△OAB=![]() ;
;
(2)结合已知条件,根据勾股定理逆定理可得△OAB是直角三角形,根据两组对边分别平行的四边形是平行的四边形可得四边形PABO是平行四边形,由平行四边形的性质可得PO=AB,即可得PC=2![]() ﹣2.
﹣2.
(1)①证明:连接OA、OB,则有OA=OB=OC,
∵PA是⊙O的切线,
∴OA⊥PA,
∵点C是PO的中点,
∴PC=OC=![]() PO,
PO,
∴OA=![]() PO,
PO,
∴在Rt△OAP中,sin∠APO=![]() =
=![]() ,
,
∴∠APO=30°,
∴∠POA=60°,
∵AB∥PO,
∴∠BAO=∠POA=60°,
∴△OAB是等边三角形,
∴AB=OA,
∴AB=PC,
∴四边形PABC是平行四边形;
②解:过点O作OE⊥AB,垂足为E,
∵△OAB是等边三角形,
∴OA=AB=2,
∴OE=OAsin60°=2×![]() =
=![]() ,
,
∴S△OAB=![]() ABOE=
ABOE=![]() ×2×
×2×![]() =
=![]() ,
,
∵AB∥PO,
∴S△PAB=S△OAB=![]() ;
;
(2)PC=2![]() ﹣2,理由为:
﹣2,理由为:
∵OA=OB=2,AB=2![]() ,
,
∴OA2+OB2=AB2,
∴根据勾股定理逆定理可得,△OAB是直角三角形,即∠AOB=90°,
∴OB∥PA,
∴四边形PABO是平行四边形,
∴PO=AB,
∴PC=2![]() ﹣2.
﹣2.


科目:初中数学 来源: 题型:
【题目】如图,点A在反比例函数y=![]() (x>0)的图像上,点B在反比例函数y=
(x>0)的图像上,点B在反比例函数y=![]() (x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
(x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )

A. 10 B. 12 C. 14 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
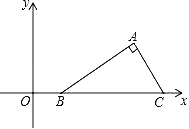
A. (﹣4,﹣2﹣![]() ) B. (﹣4,﹣2+
) B. (﹣4,﹣2+![]() ) C. (﹣2,﹣2+
) C. (﹣2,﹣2+![]() ) D. (﹣2,﹣2﹣
) D. (﹣2,﹣2﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
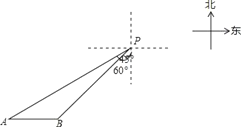
【题目】一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:![]() ≈1.732,结果精确到0.1)?
≈1.732,结果精确到0.1)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题:
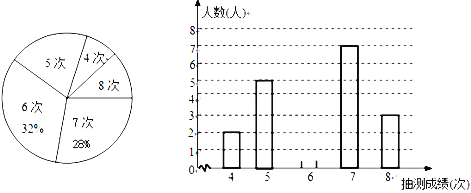
(1)本次抽测的男生有________人,抽测成绩的众数是_________;
(2)请将条形图补充完整;
(3)若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
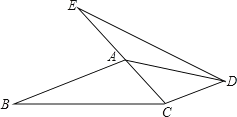
【题目】已知:如图,点E、A、C在同一条直线上,AB∥CD,AB=CE,∠B=∠E.
(1)求证:△ABC≌△CED;
(2)若∠B=25°,∠ACB=45°,求∠ADE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论为( )
,其中正确结论为( )
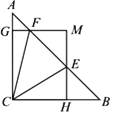
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
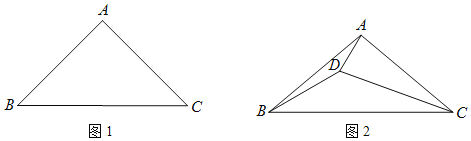
【题目】在△ABC中,AB=AC,将线段AC绕着点C逆时针旋转得到线段CD,旋转角为α.
(1)如图,∠BAC=90°,α=45°,试求点D到边AB,AC的距离的比值;
(2)如图,∠BAC=100°,α=20°,连接AD,BD,求∠CBD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某底面为圆形的古塔剖面和山坡的剖面在同一平面上,古塔EF(F为塔底的中心)与地面BD垂直,古塔的底面直径CD=8米,BC=10米,斜坡AB=26米,斜坡坡面AB的坡度i=5:12,在坡脚的点A处测得古塔顶端点E的仰角∠GAE=47°,则古塔EF的高度约( )(参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)
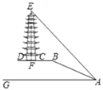
A. 27.74米B. 30.66米C. 35.51米D. 40.66米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com