
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 的重直平分线交
的重直平分线交![]() ,
,![]() 于点
于点![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的面积.
的面积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)首先连接BE,由在△ABC中,∠C=90°,∠A=30°,可求得∠ABC的度数,又由AB的垂直平分线交AB于点D,交AC于点E,根据线段垂直平分线的性质,可得AE=BE,继而可求得∠CBE的度数,然后由含30°角的直角三角形的性质,证得AE=2CE.(2) △ADE中,∠ADE=90°,∠A=30°,![]() ,推出AE=2,从而求出AC的长,再根据勾股定理求出BC的长,即可求出
,推出AE=2,从而求出AC的长,再根据勾股定理求出BC的长,即可求出![]() 的面积.
的面积.
如图,连接BE,

∵在△ABC中,∠C=90°,∠A=30°,
∴∠ABC=90°-∠A=60°,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABC-∠ABE=30°,
在Rt△BCE中,BE=2CE,
∴AE=2CE.
(2)∵△ADE中,∠ADE=90°,∠A=30°,![]() ,∴AE=2,
,∴AE=2,
∵![]() ,∴CE=1,AC=3,
,∴CE=1,AC=3,
设BC=x,则AB=2x,
∴![]()
∴BC= ![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,且DM=DN.
(1)如图甲,若∠C=90°,∠BAC=60°,AC=9,∠MDN=120°,ND∥AB.
①写出∠MDA= °,AB的长是 .
②求四边形AMDN的周长;

(2)如图乙,过D作DF⊥AC于F,先补全图乙再证明AM+AN=2AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图,在正方形![]() 和平行四边形
和平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
探究:当![]() 与
与![]() 的夹角为多少度时,平行四边形
的夹角为多少度时,平行四边形![]() 是正方形?
是正方形?
小聪同学的思路是:首先可以说明四边形![]() 是矩形;然后延长
是矩形;然后延长![]() 交
交![]() 于点
于点![]() ,构造全等三角形,经过推理可以探索出问题的答案.
,构造全等三角形,经过推理可以探索出问题的答案.
请你参考小聪同学的思路,探究并解决这个问题.

(1)求证:四边形![]() 是矩形;
是矩形;
(2)![]() 与
与![]() 的夹角为________度时,四边形
的夹角为________度时,四边形![]() 是正方形.
是正方形.
理由:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位运动员在相同条件下各射靶![]() 次,每次射靶的成绩如下:
次,每次射靶的成绩如下:
甲:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
乙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
丙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 |
|
| __________ |
乙 | __________ |
|
|
丙 |
| __________ |
|
(2)根据表中数据分析,哪位运动员的成绩最稳定.并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
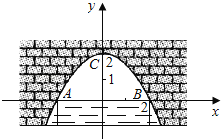
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△OAB的边长为2,点B在x轴上,反比例函数的图象经过A点,将△OAB绕点O顺时针旋转α(0°<α<360°),使点A落在双曲线上,则α=________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB为⊙O的直径,C是⊙O上一点,如图,AB=12,BC=4![]() .BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.
.BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.
(1)求CE的长;
(2)延长CE到F,使EF=![]() ,连接BF并延长BF交⊙O于点G,求BG的长;
,连接BF并延长BF交⊙O于点G,求BG的长;
(3)在(2)的条件下,连接GC并延长GC交BH于点D,求证:BD=BG.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com