
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыyжсЕФе§АыжсНЛгкЕуAЃЌгыxжсНЛгкЕу
ЕФЭМЯѓгыyжсЕФе§АыжсНЛгкЕуAЃЌгыxжсНЛгкЕу![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЖЏЕуPДгЕуBГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдкЩфЯпBOЩЯдЫЖЏЃЌЖЏЕуQДгOГіЗЂЃЌбиxжсЕФе§АыжсгыЕуPЭЌЪБвдЯрЭЌЕФЫйЖШдЫЖЏЃЌЙ§Pзї
ЖЏЕуPДгЕуBГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдкЩфЯпBOЩЯдЫЖЏЃЌЖЏЕуQДгOГіЗЂЃЌбиxжсЕФе§АыжсгыЕуPЭЌЪБвдЯрЭЌЕФЫйЖШдЫЖЏЃЌЙ§Pзї![]() жсНЛжБЯпABгкMЃЎ
жсНЛжБЯпABгкMЃЎ
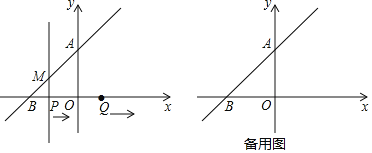
![]() ЧѓжБЯпABЕФНтЮіЪНЃЎ
ЧѓжБЯпABЕФНтЮіЪНЃЎ
![]() ЕБЕуPдкЯпЖЮOBЩЯдЫЖЏЪБЃЌЩш
ЕБЕуPдкЯпЖЮOBЩЯдЫЖЏЪБЃЌЩш![]() ЕФУцЛ§ЮЊSЃЌЕуPдЫЖЏЕФЪБМфЮЊtУыЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪН
ЕФУцЛ§ЮЊSЃЌЕуPдЫЖЏЕФЪБМфЮЊtУыЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪН![]() жБНгаДГіздБфСПЕФШЁжЕЗЖЮЇ
жБНгаДГіздБфСПЕФШЁжЕЗЖЮЇ![]() ЃЎ
ЃЎ
![]() Й§ЕуQзї
Й§ЕуQзї![]() жсНЛжБЯпABгкNЃЌдкдЫЖЏЙ§ГЬжа
жсНЛжБЯпABгкNЃЌдкдЫЖЏЙ§ГЬжа![]() ВЛгыBжиКЯ
ВЛгыBжиКЯ![]() ЃЌЪЧЗёДцдкФГвЛЪБПЬ
ЃЌЪЧЗёДцдкФГвЛЪБПЬ![]() Уы
Уы![]() ЃЌЪЙ
ЃЌЪЙ![]() ЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіЪБМфtжЕЃЎ
ЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіЪБМфtжЕЃЎ
ЁОД№АИЁП(1)yЃНx+2ЃЛ(2)SЃНt(0ЃМtЁм2)ЃЛ(3)ДцдкЃЌtЃН2Лђ2![]() Љ2ЃЎ
Љ2ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉSЁїABO=![]() ЁСOAЁСOB=
ЁСOAЁСOB=![]() ЁСAOЁС2=2ЃЌдђOA=2ЃЌМДЕуAЃЈ0ЃЌ2ЃЉЃЌМДПЩЧѓНтЃЛ
ЁСAOЁС2=2ЃЌдђOA=2ЃЌМДЕуAЃЈ0ЃЌ2ЃЉЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉtУыЪБЃЌЕуPЕФзјБъЮЊЃЈ-2+tЃЌ0ЃЉЃЌдђMP=BP=tЃЌS=![]() ЁСPQЁСMPЃЌМДПЩЧѓНтЃЛ
ЁСPQЁСMPЃЌМДПЩЧѓНтЃЛ
ЃЈ3ЃЉЗжMN=MQЁЂMN=NQЁЂMQ=NQШ§жжЧщПіЃЌЧѓНтМДПЩЃЎ
(1)SЁїABOЃН![]() ЁСOAЁСOBЃН
ЁСOAЁСOBЃН![]() ЁСAOЁС2ЃН2ЃЌдђOAЃН2ЃЌМДЕуA(0ЃЌ2)ЃЌ
ЁСAOЁС2ЃН2ЃЌдђOAЃН2ЃЌМДЕуA(0ЃЌ2)ЃЌ
НЋЕуAЁЂBЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНЃКyЃНkm+nЃЌЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЙЪжБЯпABЕФБэДяЪНЮЊЃКyЃНx+2ЃЛ
(2)tУыЪБЃЌЕуPЕФзјБъЮЊ(Љ2+tЃЌ0)ЃЌдђMPЃНBPЃНtЃЌ
SЃН![]() ЁСPQЁСMPЃН
ЁСPQЁСMPЃН![]() ЁС2tЃНt(0ЃМtЁм2)ЃЛ
ЁС2tЃНt(0ЃМtЁм2)ЃЛ
(3)ДцдкЃЌРэгЩЃК
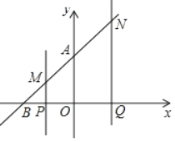
tУыЪБЃЌЕуMЁЂNЁЂQЕФзјБъЗжБ№ЮЊ(Љ2+tЃЌt)ЁЂ(tЃЌt+2)ЁЂ(tЃЌ0)ЃЌ
дђЃКMN2ЃН4+4ЃН8ЃЌMQ2ЃН4+t2ЃЌNQ2ЃН(t+2)2ЃЌ
ЕБMNЃНMQЪБЃЌМДЃК8ЃН4+t2ЃЌtЃН2(ИКжЕвбЩсШЅ)ЃЌ
ЕБMNЃНNQЪБЃЌЭЌРэПЩЕУЃКtЃН2![]() Љ2(ИКжЕвбЩсШЅ)ЃЌ
Љ2(ИКжЕвбЩсШЅ)ЃЌ
ЕБMQЃНNQЪБЃЌЭЌРэПЩЕУЃКtЃН0(ЩсШЅ)ЃЌ
ЙЪЃКЕБЁїMNQЪЧЕШбќШ§НЧаЮЪБЃЌtЃН2Лђ2![]() Љ2ЃЎ
Љ2ЃЎ


 ЦкФЉ1ОэЫижЪНЬг§ЦРЙРОэЯЕСаД№АИ
ЦкФЉ1ОэЫижЪНЬг§ЦРЙРОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіЕуЕНдВЕФзюаЁОрРыЮЊ![]() ЃЌзюДѓОрРыЮЊ
ЃЌзюДѓОрРыЮЊ![]() ЃЌдђИУдВЕФАыОЖЪЧ____________ЃЎ
ЃЌдђИУдВЕФАыОЖЪЧ____________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌADЁЮBCЃЌЁЯEADЃНЁЯCЃЎ

ЃЈ1ЃЉЪдХаЖЯAEгыCDЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЁЯFECЃНЁЯBAEЃЌЁЯEFCЃН50ЁуЃЌЧѓЁЯBЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЪЕЪ§aЃЌbЃЌcТњзу|a-![]() |+
|+![]() =
=![]() +
+![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓaЃЌbЃЌcЃЛ
ЃЈ2ЃЉШєТњзуЩЯЪНЕФaЃЌcЮЊЕШбќШ§НЧаЮЕФСНБпЃЌЧѓетИіЕШбќШ§НЧаЮЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯЃКЮвУЧбЇЙ§вЛДЮКЏЪ§ЕФЭМЯѓЕФЦНвЦЃЌШчЃКНЋвЛДЮКЏЪ§![]() ЕФЭМЯѓбиxжсЯђгвЦНвЦ1ИіЕЅЮЛГЄЖШПЩЕУЕНКЏЪ§
ЕФЭМЯѓбиxжсЯђгвЦНвЦ1ИіЕЅЮЛГЄЖШПЩЕУЕНКЏЪ§![]() ЕФЭМЯѓЃЌдйбиyжсЯђЩЯЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНКЏЪ§
ЕФЭМЯѓЃЌдйбиyжсЯђЩЯЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНКЏЪ§![]() ЕФЭМЯѓЃЛШчЙћНЋвЛДЮКЏЪ§
ЕФЭМЯѓЃЛШчЙћНЋвЛДЮКЏЪ§![]() ЕФЭМЯѓбиxжсЯђзѓЦНвЦ1ИіЕЅЮЛГЄЖШПЩЕУЕНКЏЪ§
ЕФЭМЯѓбиxжсЯђзѓЦНвЦ1ИіЕЅЮЛГЄЖШПЩЕУЕНКЏЪ§![]() ЕФЭМЯѓЃЌдйбиyжсЯђЯТЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНКЏЪ§
ЕФЭМЯѓЃЌдйбиyжсЯђЯТЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНКЏЪ§![]() ЕФЭМЯѓЃЛЗТееЩЯЪіЦНвЦЕФЙцТЩЃЌНтОіЯТСаЮЪЬтЃК
ЕФЭМЯѓЃЛЗТееЩЯЪіЦНвЦЕФЙцТЩЃЌНтОіЯТСаЮЪЬтЃК
![]() НЋвЛДЮКЏЪ§
НЋвЛДЮКЏЪ§![]() ЕФЭМЯѓбиxжсЯђгвЦНвЦ3ИіЕЅЮЛГЄЖШЃЌдйбиyжсЯђЩЯЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНКЏЪ§ЕФЭМЯѓЃЛ
ЕФЭМЯѓбиxжсЯђгвЦНвЦ3ИіЕЅЮЛГЄЖШЃЌдйбиyжсЯђЩЯЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНКЏЪ§ЕФЭМЯѓЃЛ
![]() НЋ
НЋ![]() ЕФКЏЪ§ЭМЯѓбиyжсЯђЯТЦНвЦ3ИіЕЅЮЛГЄЖШЃЌЕУЕНКЏЪ§ЕФЭМЯѓЃЌдйбиxжсЯђзѓЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНКЏЪ§ЕФЭМЯѓЃЛ
ЕФКЏЪ§ЭМЯѓбиyжсЯђЯТЦНвЦ3ИіЕЅЮЛГЄЖШЃЌЕУЕНКЏЪ§ЕФЭМЯѓЃЌдйбиxжсЯђзѓЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНКЏЪ§ЕФЭМЯѓЃЛ
![]() КЏЪ§
КЏЪ§![]() ЕФЭМЯѓПЩгЩ
ЕФЭМЯѓПЩгЩ![]() ЕФЭМЯѓОЙ§дѕбљЕФЦНвЦБфЛЛЕУЕНЃП
ЕФЭМЯѓОЙ§дѕбљЕФЦНвЦБфЛЛЕУЕНЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌдкЕШБпЁїABCжаЃЌЕуDЁЂEЗжБ№дкБпBCЁЂABЩЯЃЌЧв BD=AEЃЌADгыCEНЛгкЕу ![]() ЃЎ
ЃЎ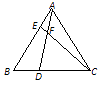
ЃЈ1ЃЉЪдЫЕУї ![]() ЕФРэгЩЃЛ
ЕФРэгЩЃЛ
ЃЈ2ЃЉЧѓ ![]() ЕФЖШЪ§ЃЎ
ЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,вбжЊA(3ЃЌ0),B(0ЃЌ-1)ЃЌСЌНгAB,Й§BЕузїABЕФДЙЯпЖЮ,ЪЙBA=BC,СЌНгAC.
(1)ШчЭМ1ЃЌЧѓCЕузјБъЃЛ
(2)ШчЭМ2,ШєPЕуДгAЕуГіЗЂ,биxжсЯђзѓЦНвЦ,СЌНгBP,зїЕШбќжБНЧШ§НЧаЮЁїBPQ,СЌНгCQ.ЧѓжЄ:PA=CQ.
(3)дк(2)ЕФЬѕМўЯТ,ШєCЁЂPЁЂQШ§ЕуЙВЯп,ЧѓДЫЪБPЕузјБъМАЁЯAPBЕФЖШЪ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇбЇЩњВНааЕННМЭтТУааЃЌЦпФъМЖ![]() АрбЇЩњзщГЩЧАЖгЃЌВНааЫйЖШЮЊ4ЧЇУз
АрбЇЩњзщГЩЧАЖгЃЌВНааЫйЖШЮЊ4ЧЇУз![]() аЁЪБЃЌЦп
аЁЪБЃЌЦп![]() АрЕФбЇЩњзщГЩКѓЖгЃЌЫйЖШЮЊ6ЧЇУз
АрЕФбЇЩњзщГЩКѓЖгЃЌЫйЖШЮЊ6ЧЇУз![]() аЁЪБЃЛЧАЖгГіЗЂ1аЁЪБКѓЃЌКѓЖгВХГіЗЂЃЌЭЌЪБКѓЖгХЩвЛУћСЊТчдБЦяздааГЕдкСНЖгжЎМфВЛМфЖЯЕиРДЛиСЊТчЃЌЫћЦяГЕЕФЫйЖШЮЊ10ЧЇУз
аЁЪБЃЛЧАЖгГіЗЂ1аЁЪБКѓЃЌКѓЖгВХГіЗЂЃЌЭЌЪБКѓЖгХЩвЛУћСЊТчдБЦяздааГЕдкСНЖгжЎМфВЛМфЖЯЕиРДЛиСЊТчЃЌЫћЦяГЕЕФЫйЖШЮЊ10ЧЇУз![]() аЁЪБЃЎ
аЁЪБЃЎ
![]() КѓЖгзЗЩЯЧАЖгашвЊЖрГЄЪБМфЃП
КѓЖгзЗЩЯЧАЖгашвЊЖрГЄЪБМфЃП
![]() КѓЖгзЗЩЯЧАЖгЕФЪБМфФкЃЌСЊТчдБзпЕФТЗГЬЪЧЖрЩйЃП
КѓЖгзЗЩЯЧАЖгЕФЪБМфФкЃЌСЊТчдБзпЕФТЗГЬЪЧЖрЩйЃП
![]() ЦпФъМЖ
ЦпФъМЖ![]() АрГіЗЂЖрЩйаЁЪБКѓСНЖгЯрОр2ЧЇУзЃП
АрГіЗЂЖрЩйаЁЪБКѓСНЖгЯрОр2ЧЇУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
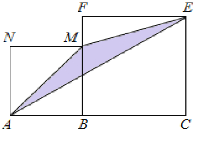
ЁОЬтФПЁПШчЭМЃЌЕуBдкЯпЖЮACЩЯЃЈBC>ABЃЉЃЌдкЯпЖЮACЭЌВрзїе§ЗНаЮABMNМАе§ЗНаЮBCEFЃЌСЌНгAMЁЂMEЁЂEAЕУЕНЁїAMEЃЎЕБAB=1ЪБЃЌЁїAMEЕФУцЛ§МЧЮЊS1ЃЛЕБAB=2ЪБЃЌЁїAMEЕФУцЛ§МЧЮЊS2ЃЛЕБAB=3ЪБЃЌЁїAMEЕФУцЛ§МЧЮЊS3ЃЛдђS2020ЉS2019=_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com