
【题目】将线段![]() 绕点
绕点![]() 逆时针旋转角度
逆时针旋转角度![]() 得到线段
得到线段![]() ,连接
,连接![]() 得
得![]() ,又将线段
,又将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() (如图①).
(如图①).
![]() 求
求![]() 的大小(结果用含
的大小(结果用含![]() 的式子表示);
的式子表示);
![]() 又将线段
又将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得线段
得线段![]() ,连接
,连接![]() (如图②)求
(如图②)求![]() ;
;
![]() 连接
连接![]() 、
、![]() ,试探究当
,试探究当![]() 为何值时,
为何值时,![]() .
.

【答案】![]()
![]() ;
;![]()
![]() ;
;![]() 当
当![]() 为
为![]() 时,
时,![]() .
.
【解析】
(1)由于线段AB绕点A逆时针旋转角度α(0°<α<60°)得到线段AC,根据旋转的性质得AB=AC,∠BAC=α,利用等腰三角形的性质和三角形内角和定理得到∠ABC=∠ACB=90°﹣![]() α,再由线段BC绕点B逆时针旋转60°得线段BD,根据旋转的性质得∠CBD=60°,然后利用∠ABD=∠ABC﹣∠CBD进行计算;
α,再由线段BC绕点B逆时针旋转60°得线段BD,根据旋转的性质得∠CBD=60°,然后利用∠ABD=∠ABC﹣∠CBD进行计算;
(2)由线段AB绕点B顺时针旋转60°得线段BE,根据旋转的性质得AB=AE,∠BAE=60°,则AC=AE,∠CAE=60°﹣α,利用等腰三角形的性质和三角形内角和得到∠ACE=∠AEC=60°+![]() α,然后利用∠BCE=∠ACB+∠ACE计算得到∠BCE=150°;
α,然后利用∠BCE=∠ACB+∠ACE计算得到∠BCE=150°;
(3)由线段BC绕点B逆时针旋转60°得线段BD,根据旋转的性质得BC=BD,∠CBD=60°,则可判断△BCD为等腰直角三角形,则∠BCD=60°,CD=BC,所以∠DCE=∠BCE﹣∠BCD=90°,加上∠DEC=45°,于是△DEC为等腰直角三角形,则CE=CD,所以CB=CE,然后利用“SSS”证明△ABC≌△AEC,得到∠BAC=∠EAC,所以α=![]() ∠BAE=30°.
∠BAE=30°.
(1)∵线段AB绕点A逆时针旋转角度α(0°<α<60°)得到线段AC,∴AB=AC,∠BAC=α,∴∠ABC=∠ACB,∴∠ABC=∠ACB=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α.
α.
∵线段BC绕点B逆时针旋转60°得线段BD,∴∠CBD=60°,∴∠ABD=∠ABC﹣∠CBD=90°﹣![]() α﹣60°=30°﹣
α﹣60°=30°﹣![]() α(0°<α<60°);
α(0°<α<60°);
(2)∵线段AB绕点B顺时针旋转60°得线段BE,∴AB=AE,∠BAE=60°,∴AC=AE,∠CAE=60°﹣α,∴∠ACE=∠AEC=![]() (180°﹣60°+α)=60°+
(180°﹣60°+α)=60°+![]() α,∴∠BCE=∠ACB+∠ACE=90°﹣
α,∴∠BCE=∠ACB+∠ACE=90°﹣![]() α+60°+
α+60°+![]() α=150°;
α=150°;
(3)如图②.
∵线段BC绕点B逆时针旋转60°得线段BD,∴BC=BD,∠CBD=60°,∴△BCD为等边三角形,∴∠BCD=60°,CD=BC,∴∠DCE=∠BCE﹣∠BCD=150°﹣60°=90°.
∵∠DEC=45°,∴△DEC为等腰直角三角形,∴CE=CD,∴CB=CE.
在△ABC和△AEC中,∵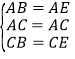 ,∴△ABC≌△AEC(SSS),∴∠BAC=∠EAC,∴∠BAC=
,∴△ABC≌△AEC(SSS),∴∠BAC=∠EAC,∴∠BAC=![]() ∠BAE=30°,即α=30°.
∠BAE=30°,即α=30°.
故当α为30°时,∠DEC=45°.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图1,在![]() 和
和![]() 中,
中, ![]() ,
,![]() ,
,![]() .
.

(1)若![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
(2)在第(1)问的条件下,求证: ![]() ;
;
(3)将![]() 绕点
绕点![]() 顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为________;
②该函数的一条性质:__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ,
,![]() 、
、![]() 、
、![]() 为常数)的图象如图所示,下列
为常数)的图象如图所示,下列![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 为常数,且
为常数,且![]() .其中正确的结论有( )
.其中正确的结论有( )
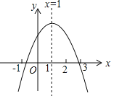
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在直线l上,点B在直线l外,点B关于直线l的对称点为C,连接AC,过点B作BD⊥AC于点D,延长BD至E使BE=AB,连接AE并延长与BC的延长线交于点F.

(1)补全图形;
(2)若∠BAC=2α,求出∠AEB的大小(用含α的式子表示);
(3)用等式表示线段EF与BC的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读“末位数字是![]() 的两位数平方的速算法则”,并完成下列问题.
的两位数平方的速算法则”,并完成下列问题.
通过计算器计算可得:![]() .容易发现这样的速算法则:末位数字是
.容易发现这样的速算法则:末位数字是![]() 的两位数的平方,可以先写出它的十位数字与其下一个自然数的乘积,再在末位接着写上
的两位数的平方,可以先写出它的十位数字与其下一个自然数的乘积,再在末位接着写上![]() .例如:计算
.例如:计算![]() ,因为
,因为![]() ,在
,在![]() 的后面接着写上
的后面接着写上![]() ,所以
,所以![]() ;计算
;计算![]() ;因为
;因为![]() ,在
,在![]() 的后面接着写上
的后面接着写上![]() ,所以
,所以![]() .
.
(1)用学过的整式的乘法来验证“末位数字是![]() 的两位数平方的速算法则”是否正确:
的两位数平方的速算法则”是否正确:
第一步:我们设末位数字是![]() 的两位数中的十位数字为
的两位数中的十位数字为![]() ,这个两位数用含
,这个两位数用含![]() 的代数式表示为_____,则它的平方为 ( 请把平方结果计算出来并化简);
的代数式表示为_____,则它的平方为 ( 请把平方结果计算出来并化简);
第二步:依据文中“先写出它的十位数字与其下一个自然数的乘积,再在末位接着写上25"这一句话,用含n的代数式表示速算计算结果为 ,这个代数式化简后为 ;
第三步:因为第一步和第二步最终得到的代数式结果相等,所以得出速算法则是“正确”的结论
(2)如果计算的是末位数字是![]() 的三位数、四位数···,这个速算法则 (填“成立”或“不成立”).
的三位数、四位数···,这个速算法则 (填“成立”或“不成立”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划从商店购进![]() 两种商品,购买一个
两种商品,购买一个![]() 商品比购买一个
商品比购买一个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)根据学校实际情况,该学校需要购买![]() 种商品的个数是购买
种商品的个数是购买![]() 种商品个数的3倍,还多11个,经与商店洽谈,商店决定在该学校购买
种商品个数的3倍,还多11个,经与商店洽谈,商店决定在该学校购买![]() 种商品时给予八折优惠,如果该学校本次购买
种商品时给予八折优惠,如果该学校本次购买![]() 两种商品的总费用不超过1000元,那么该学校最多可购买多少个
两种商品的总费用不超过1000元,那么该学校最多可购买多少个![]() 种商品?
种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,以线段
,以线段![]() 为直角边在第一象限内作等腰直角三角形
为直角边在第一象限内作等腰直角三角形![]() ,
,![]() ,点
,点![]() 为坐标系中的一个动点.
为坐标系中的一个动点.

(1)请直接写出直线![]() 的表达式;
的表达式;
(2)求出![]() 的面积;
的面积;
(3)当![]() 与
与![]() 面积相等时,求实数
面积相等时,求实数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.

(1)求证:DA∥BC;
(2)猜想线段DF、AF的数量关系,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com