
【题目】如图,已知△ABC内接于⊙O中,AB=![]() ,∠C=60°.
,∠C=60°.
(1)求⊙O的半径;
(2) 若∠CAB=45°,点P从C点出发,沿 弧 CA 向点A滑动,滑动多长距离时△PAB会是等边三角形?
【答案】(1)2;(2)点P 滑动 ![]() 时,△PAB会是等边三角形.
时,△PAB会是等边三角形.
【解析】
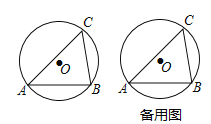
(1)作直径AD,连接BD,如图1,利用圆周角定理得到∠ABD=90°,∠D=∠C=60°,然后在在Rt△ABD中利用∠D的正弦可计算出AD,从而得到⊙O的半径;
(2)如图2,△PAB为等边三角形,连接PO、PC,利用等边三角形的性质得∠PAB=60°,则∠PAC=15°,根据圆周角定理得到∠POC=2∠PAC=30°,然后利用弧长公式计算![]() 的长度即可.
的长度即可.
(1)作直径AD,连接BD,如图1.
∵AD为直径,∴∠ABD=90°.
∵∠D=∠C=60°.在Rt△ABD中,∵sinD![]() ,∴AD
,∴AD![]() 4,∴⊙O的半径为2;
4,∴⊙O的半径为2;
(2)如图2,△PAB为等边三角形,连接PO、PC,∴∠PAB=60°,∴∠PAC=∠PAB﹣∠CAB=60°﹣45°=15°,∴∠POC=2∠PAC=30°,∴![]() 的长度
的长度![]() π,即点P滑动
π,即点P滑动![]() π距离时△PAB会是等边三角形.
π距离时△PAB会是等边三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
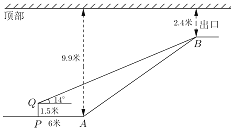
【题目】地铁10号线某站点出口横截面平面图如图所示,电梯![]() 的两端分别距顶部9.9米和2.4米,在距电梯起点
的两端分别距顶部9.9米和2.4米,在距电梯起点![]() 端6米的
端6米的![]() 处,用1.5米的测角仪测得电梯终端
处,用1.5米的测角仪测得电梯终端![]() 处的仰角为14°,求电梯
处的仰角为14°,求电梯![]() 的坡度与长度.(参考数据:
的坡度与长度.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
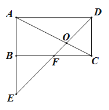
【题目】如图所示,在矩形ABCD中,点F是 BC的中点,DF的延长线与AB的延长线相交于点E,DE与AC相交于点O,若![]() ,则
,则![]() ( )
( )
A. 4 B. 6 C. 8 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
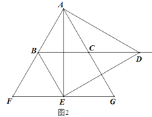
【题目】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
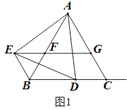
(1) 如图1,当点D在线段BC上时:
①求证:△AEB≌△ADC;②求证:四边形BCGE是平行四边形;
(2)如图2,当点D在BC的延长线上,且CD=BC时,试判断四边形BCGE是什么特殊的四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
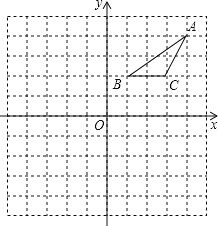
【题目】在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A、B、C的坐标分别是A(4,4)、B(1,2)、C(3,2),请解答下列问题.
(1)将△ABC向下平移5个单位长度,画出平移后的△A1B1C1;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点O逆时针旋转90°,画出旋转后的△A3B3C3.并写出点A3的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象如下所示,下列5个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() (
(![]() 的实数),其中正确的结论有几个?
的实数),其中正确的结论有几个?
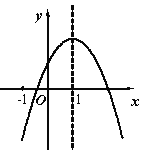
A. ①②③ B. ②③④ C. ②③⑤ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
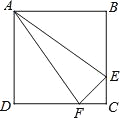
A. 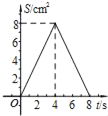 B.
B. 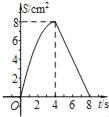
C. 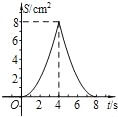 D.
D. 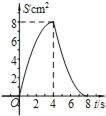
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1的![]() 的圆心A在抛物线y=(x-3)2-1上,AB//x轴交
的圆心A在抛物线y=(x-3)2-1上,AB//x轴交 ![]() 于点B(点B在点A的右侧),当点A在抛物线上运动时,点B随之运动得到的图象的函数表达式为( )
于点B(点B在点A的右侧),当点A在抛物线上运动时,点B随之运动得到的图象的函数表达式为( )

A. y=(x-4)2-1 B. y=(x-3)2 C. y=(x-2)2-1 D. y=(x-3)2-2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com