
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),(![]() ,y2)是抛物线上两点,则y1>y2,其中正确的个数是( )
,y2)是抛物线上两点,则y1>y2,其中正确的个数是( )
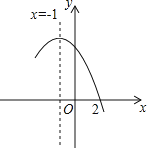
A. 1个B. 2个C. 3个D. 4个
科目:初中数学 来源: 题型:
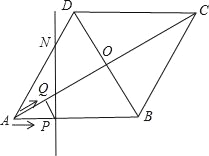
【题目】如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2![]() cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
(1)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
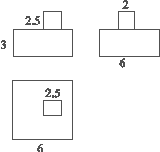
【题目】已知一个模型的三视图如图所示(单位:m).
(1)请描述这个模型的形状;
(2)若制作这个模型的木料密度为360 kg/m3,则这个模型的质量是多少?
(3)如果用油漆漆这个模型,每千克油漆可以漆4 m2,那么需要多少千克油漆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:x2﹣6x=(x2﹣6x+9)﹣9=(x﹣3)2﹣9;﹣x2+10=﹣(x2﹣10x+25)+25=﹣(x﹣5)2+25,这一种方法称为配方法,利用配方法请解以下各题:
(1)按上面材料提示的方法填空:a2﹣4a= = .﹣a2+12a= = .
(2)探究:当a取不同的实数时在得到的代数式a2﹣4a的值中是否存在最小值?请说明理由.
(3)应用:如图.已知线段AB=6,M是AB上的一个动点,设AM=x,以AM为一边作正方形AMND,再以MB、MN为一组邻边作长方形MBCN.问:当点M在AB上运动时,长方形MBCN的面积是否存在最大值?若存在,请求出这个最大值;否则请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
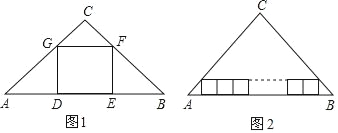
【题目】在△ABC中,∠C=90°,AC=4,BC=3,如图1,四边形DEFG为△ABC的内接正方形,则正方形DEFG的边长为_____.如图2,若三角形ABC内有并排的n个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
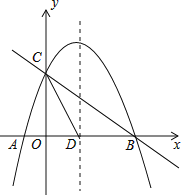
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知![]() ,
,![]() .
.
![]() 求抛物线的表达式;
求抛物线的表达式;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
![]() 点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
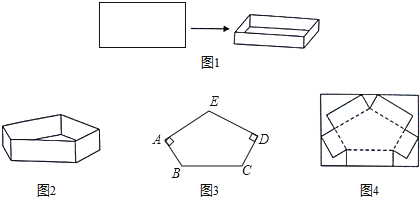
【题目】综合与实践:制作无盖盒子
任务一:如图1,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折成高为4cm,容积为![]() 的无盖长方体盒子
的无盖长方体盒子![]() 纸板厚度忽略不计
纸板厚度忽略不计![]() .
.
![]() 请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.
请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.
![]() 请求出这块矩形纸板的长和宽.
请求出这块矩形纸板的长和宽.
任务二:图2是一个高为4cm的无盖的五棱柱盒子![]() 直棱柱
直棱柱![]() ,图3是其底面,在五边形ABCDE中,
,图3是其底面,在五边形ABCDE中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 试判断图3中AE与DE的数量关系,并加以证明.
试判断图3中AE与DE的数量关系,并加以证明.
![]() 图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果
图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果![]() 图中实线表示剪切线,虚线表示折痕
图中实线表示剪切线,虚线表示折痕![]() 纸板厚度及剪切接缝处损耗忽略不计
纸板厚度及剪切接缝处损耗忽略不计![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() 此时可以得到数字密码171920.
此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
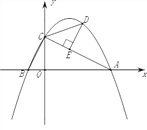
【题目】已知直线y=-![]() x+2与x轴、y轴分别交于点A、C,抛物线y=-
x+2与x轴、y轴分别交于点A、C,抛物线y=-![]() x2+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作
x2+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作![]() 于点E.
于点E.
(1)求抛物线的表达式;
(2)求△ACD面积的最大值;
(3)若△CED与△COB相似,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com