
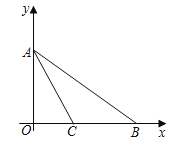
【题目】如图![]() ,在
,在![]() 中,
中,![]() 是原点,
是原点,![]() 是
是![]() 的角平分线.
的角平分线.
![]() 确定
确定![]() 所在直线的函数表达式;
所在直线的函数表达式;
![]() 在线段
在线段![]() 上是否有一点
上是否有一点![]() ,使点
,使点![]() 到
到![]() 轴和
轴和![]() 轴的距离相等,若存在,求出
轴的距离相等,若存在,求出![]() 点的坐标;若不存在,请说明理由;
点的坐标;若不存在,请说明理由;
![]() 在线段
在线段![]() 上是否有一点
上是否有一点![]() ,使点
,使点![]() 到点
到点![]() 和点
和点![]() 的距离相等,若存在,直接写出点
的距离相等,若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)存在,,
;(3)存在,,![]()
【解析】
(1)设![]() 的表达式为:
的表达式为: ![]() ,将A、B的坐标代入即可求出直线AB的解析式;
,将A、B的坐标代入即可求出直线AB的解析式;
(2)过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,根据角平分线的性质可得
,根据角平分线的性质可得![]() ,然后根据勾股定理求出AB,利用
,然后根据勾股定理求出AB,利用![]() 即可求出点C的坐标,利用待定系数法求出AC的解析式,设
即可求出点C的坐标,利用待定系数法求出AC的解析式,设![]() ,代入解析式中即可求出点P的坐标;
,代入解析式中即可求出点P的坐标;
(3)根据AC的解析式设点Q的坐标为(b,![]() ),然后利用平面直角坐标系中任意两点之间的距离公式求出QA和QB,然后利用QA=QB列方程即可求出点Q的坐标.
),然后利用平面直角坐标系中任意两点之间的距离公式求出QA和QB,然后利用QA=QB列方程即可求出点Q的坐标.
![]() 由题意得,设
由题意得,设![]() 的表达式为:
的表达式为: ![]()
将![]() 代入得,
代入得,
![]()
解得:
![]()
![]() 存在
存在
过点![]() 作
作![]() 交
交![]() 于
于![]()

![]() 是角平分线
是角平分线
![]()
在Rt△AOB中,![]()
由题意得
![]()
即有![]()
解得![]()
∴点C的坐标为:![]()
设直线AC的表达式为![]()
将![]() 代入,得
代入,得
![]()
解得:![]()
![]() 的表达式为
的表达式为![]()
设![]() ,代入
,代入![]() 得,
得,![]()
![]()
![]() 存在
存在
点Q在AC上,设点Q的坐标为(b,![]() )
)
∴QA=![]() ,
,
QB=![]()
∵QA=QB
∴![]()
解得:b=![]()
∴![]()


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点△ABC的顶点A、C的坐标分别为(﹣4,5)、(﹣1,3).
(1)请在图中正确作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 ,△A′B′C′的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,对角线AC、BD交于O,Q为CD上任意一点,AQ交BD于M,过M作MN⊥AM交BC于N,连AN、QN.下列结论:①MA=MN;②∠AQD=∠AQN; ③S△AQN=![]() S五边形ABNQD;④QN是以A为圆心,以AB为半径的圆的切线.其中正确的结论有( )
S五边形ABNQD;④QN是以A为圆心,以AB为半径的圆的切线.其中正确的结论有( )

A. ①②③④ B. 只有①③④ C. 只有②③④ D. 只有①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮政部门规定:信函重100克以内(包括100克)每20克贴邮票0.8元,不足20克重以20克计算;超过100克,先贴邮票4元,超过100克部分每100克加贴邮票2元,不足100克重以100克计算.八(9)班有11位同学参加项目化学习知识竞赛,若每份答卷重12克,每个信封重4克,将这11份答卷分装在两个信封中寄出,所贴邮票的总金额最少是_________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
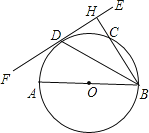
【题目】如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD

(1)用直尺和圆规作![]() 的平分线CP,CP交AB于点E(保留作图痕迹,不写作法)
的平分线CP,CP交AB于点E(保留作图痕迹,不写作法)
(2)在(1)中作出的线段CE上取一点F,连结AF.要使△ACF≌△AEF,还需要添加一个什么条件?请你写出这个条件(只要给出一种情况即可;图中不再增加字母和线段;不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△CDE都是等边三角形,且点A、C、E在一条直线上,AD与BE交于点O,AD与BC交于点P,CD与BE交于点Q,连接PQ
(1)求证:AD=BE;
(2)∠AOB的度数为 ;PQ与AE的位置关系是 ;
(3)如图2,△ABC固定,将△CDE绕点C按顺时针(或逆时针)方向旋转任意角度α,在旋转过程中,(1)中的结论是否总成立?∠AOB的度数是否改变?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
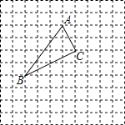
【题目】如图,在正方形网格中,每个小方格的边长都为1,△![]() 各顶点都在格点上.若点
各顶点都在格点上.若点![]() 的坐标为(0,3),请按要求解答下列问题:
的坐标为(0,3),请按要求解答下列问题:
(1)在图中建立符合条件的平面直角坐标系;
(2)根据所建立的坐标系,写出点![]() 和点
和点![]() 的坐标;
的坐标;
(3)画出△![]() 关于
关于![]() 轴的对称图形△
轴的对称图形△![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=![]() 相交于点A(m,6)和点B(﹣3,n),直线AB与y轴交于点C.
相交于点A(m,6)和点B(﹣3,n),直线AB与y轴交于点C.
(1)求直线AB的表达式;
(2)求AC:CB的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com