
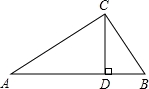
如图,在Rt△ABC中,∠C=90°,CD⊥AB,D为垂足,且BC:AC=2:3,那么BD:AD=( )
A.2:3 B.4:9 C.2:5 D.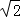 :
: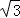
B【考点】相似三角形的判定与性质.
【分析】首先证明△BCD∽△CAD,然后根据相似三角形的面积比等于相似比的平方,可知△BCD与△CAD的面积比为(BC:AC)2=4:9,又△BCD与△CAD可看作同高(高为CD)的两个三角形,则它们的面积比等于底之比,从而得出结果.
【解答】解:∵∠ACB=90°,CD⊥AB,
∴∠BDC=∠CDA=90°,
∠B=∠ACD=90°﹣∠BCD,
∴△BCD∽△CAD,
∴△BCD的面积:△CAD的面积=(BC:AC)2=4:9.
又∵△BCD的面积:△CAD的面积=( ×BD×CD):(
×BD×CD):( ×AD×CD)=BD:AD,
×AD×CD)=BD:AD,
∴BD:AD=4:9.
故选B.
【点评】本题主要考查了相似三角形的判定、性质及同高的两个三角形的面积比等于底之比.有两角对应相等的两个三角形相似.相似三角形的面积比等于相似比的平方.


科目:初中数学 来源: 题型:
运动会前夕,爸爸陪小明在400m的环形跑道上训练,他们在同一地点沿着同一方向同
时出发.
 | |||
 | |||


(1)请根据他们的对话内容,求出小明和爸爸的速度;
(2)爸爸追上小明后,在第二次相遇前,再经过 分钟,小明和爸爸在跑道上相距50m.
查看答案和解析>>
科目:初中数学 来源: 题型:
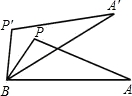
如图,如果△APB绕点B按逆时针方向旋转30°后得到△A′P′B,且BP=2,那么PP′的长为__________.(不取近似值.以下数据供解题使用:sin15°=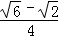 ,cos15°=
,cos15°=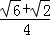 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
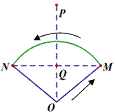
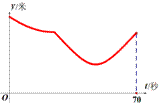
小阳在如图①所示的扇形舞台上沿O-M-N匀速行走,他从点O出发,沿箭头所示的方向经过点M再走到点N,共用时70秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走路的时间为t(单位:秒),他与摄像机的距离为y(单位:米),表示y与t的函数关系的图象大致如图②,则这个固定位置可能是图①中的
A. 点Q B. 点P C. 点M D. 点N
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com