
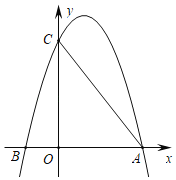
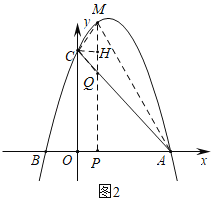
【题目】如图,平面直角坐标系中,抛物线y=﹣![]() (x﹣3a)(x+a)交x轴分别于点A、B(点B在x轴负半轴,OA>OB),交y轴于点C,OC=4OB,连接AC,点P从点A出发向点O运动,点Q从点A出发向点C运动.
(x﹣3a)(x+a)交x轴分别于点A、B(点B在x轴负半轴,OA>OB),交y轴于点C,OC=4OB,连接AC,点P从点A出发向点O运动,点Q从点A出发向点C运动.
(1)求a的值;
(2)点P、Q都以每秒1个单位的速度运动,运动t秒时,点A关于直线PQ对称的点E恰好在抛物线上,求t的值;
(3)点P以每秒1个单位的速度运动,点Q以每秒![]() 个单位的速度运动,直线PQ交抛物线于点M,当△CMA的内心在直线PQ上时,求点M的坐标.
个单位的速度运动,直线PQ交抛物线于点M,当△CMA的内心在直线PQ上时,求点M的坐标.
【答案】(1)a=1;(2)![]() ;(3)点M的坐标为(
;(3)点M的坐标为(![]() ,5)
,5)
【解析】
(1)由题意,可求得A(3a,0),B(﹣a,0),C(0,4a2),因为OC=4OB,得4a2=4a,即可得出a的值;
(2)作EH⊥AB于H,证明四边形PAQE为菱形,可得tan∠EPH=tan∠CAO=![]() ,设EH=4m,PH=3m,则PA=PE=5m,所以点E的坐标为(3﹣8m,4m),代入抛物线y=﹣
,设EH=4m,PH=3m,则PA=PE=5m,所以点E的坐标为(3﹣8m,4m),代入抛物线y=﹣![]() (x﹣3)(x+1),求得m的值,即可得出t的值;
(x﹣3)(x+1),求得m的值,即可得出t的值;
(3)连接MA,MC,作CH⊥MP于H,设运动时间为t秒,则AP=t,AQ=![]() ,可得PM∥CO,当△CMA的内心在直线PQ上时,证明△CHM∽△APM,得
,可得PM∥CO,当△CMA的内心在直线PQ上时,证明△CHM∽△APM,得![]() ,即
,即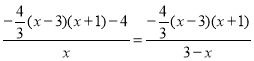 ,解方程求得x的值,即可得出点M的坐标.
,解方程求得x的值,即可得出点M的坐标.
解:(1)∵抛物线y=﹣![]() (x﹣3a)(x+a)交x轴分别于点A、B(点B在x轴负半轴,OA>OB),
(x﹣3a)(x+a)交x轴分别于点A、B(点B在x轴负半轴,OA>OB),
当y=0时,x=3a或x=﹣a,
当x=0时,y=4a2
∴A(3a,0),B(﹣a,0),C(0,4a2),
∵OC=4OB,
∴4a2=4a,
∴a=1或a=0(舍去),
∴a=1.
(2)如图1,作EH⊥AB于H,
∴点A关于直线PQ对称的点E恰好在抛物线上,
∴PA=PE,QA=QE,
∵AP=AQ=t,
∴PA=PE=QE=QA,
∴四边形PAQE为菱形,
∴EP∥AC,
∴∠EPH=∠CAO,
∵A(3,0),C(0,4),
∴tan∠EPH=tan∠CAO=![]() ,
,
设EH=4m,PH=3m,则PA=PE=5m,
∴点E的坐标为(3﹣8m,4m),
代入抛物线y=﹣![]() (x﹣3)(x+1),得4m=
(x﹣3)(x+1),得4m=![]() ×(﹣8m)×(4﹣8m),
×(﹣8m)×(4﹣8m),
∵m>0,解得m=![]() ,
,
∴t=5a=![]() ;
;
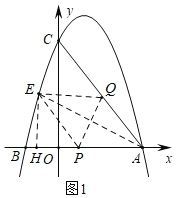
(3)如图2,连接MA,MC,作CH⊥MP于H,
设运动时间为t秒,则AP=t,AQ=![]() ,
,
∴![]() ,
,
∴PM∥CO,
当△CMA的内心在直线PQ上时,有∠CMH=∠AMP,
∵∠CHM=∠APM=90°,
∴△CHM∽△APM,
∴![]() ,
,
∴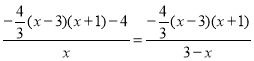 ,
,
化简,得![]() ,解得x=
,解得x=![]() ,
,
∴y=![]()
∴点M的坐标为(![]() ,5).
,5).


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上的第一象限内的动点,过点P作PMx轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.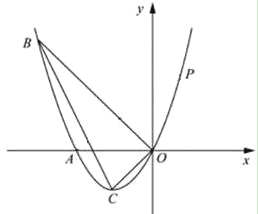
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球然后放回,再随机摸出一个小球.
(Ⅰ)请用列表法(或画树状图法)列出所有可能的结果;
(Ⅱ)求两次取出的小球标号相同的概率;
(Ⅲ)求两次取出的小球标号的和大于6的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
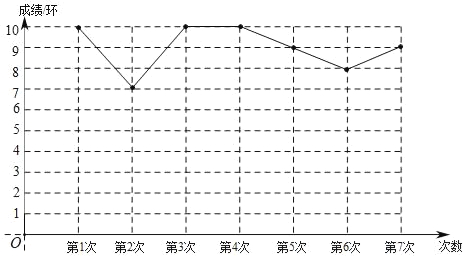
【题目】嘉淇同学利用业余时间进行射击训练,一共射击7次,经过统计,制成如图12所示的折线统计图.
(1)这组成绩的众数是 ;
(2)求这组成绩的方差;
(3)若嘉淇再射击一次(成绩为整数环),得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数,求第8次的射击成绩的最大环数.
查看答案和解析>>
科目:初中数学 来源: 题型:
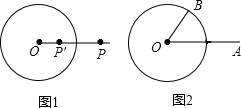
【题目】如图1,⊙O的半径为r,若点P′在射线OP上,满足OP′×OP=r2,则称点P′是点P关于⊙O的“反演点”,如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A'是点A关于⊙O的反演点,求A'B的长为( )
A.![]() B.2
B.2![]() C.2D.4
C.2D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题发现]
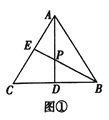
如图①,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,
上,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,则
,则![]() _____ ;
_____ ;
[拓展提高]
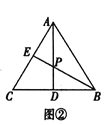
如图②,在等边三角形![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,直线
上,直线![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
[解决问题]
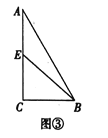
如图③,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,![]() .请直接写出
.请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
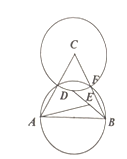
【题目】如图,已知等边△ABC的边长为4,以AB为直径的圆交BC于点F,CF为半径作圆,D是⊙C上一动点,E是BD的中点,当AE最大时,BD的长为( )
A.![]() B.
B.![]() C.4D.6
C.4D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
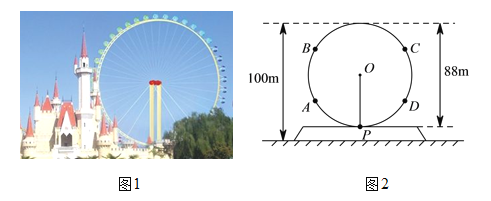
【题目】某游乐园的摩天轮(如图1)有均匀分布在圆形转轮边缘的若干个座舱,人们坐在座舱中可以俯瞰美景,图2是摩天轮的示意图.摩天轮以固定的速度绕中心![]() 顺时针方向转动,转一圈为
顺时针方向转动,转一圈为![]() 分钟.从小刚由登舱点
分钟.从小刚由登舱点![]() 进入摩天轮开始计时,到第12分钟时,他乘坐的座舱到达图2中的点_________处(填
进入摩天轮开始计时,到第12分钟时,他乘坐的座舱到达图2中的点_________处(填![]() ,
,![]() ,
,![]() 或
或![]() ),此点距地面的高度为_______m.
),此点距地面的高度为_______m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com