
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 的中点
的中点![]() 为圆心,以
为圆心,以![]() 的长为直径的
的长为直径的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() ,交
,交![]() 于点
于点![]() .
.
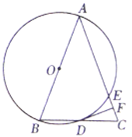
(1)求证:![]() ;
;
(2)填空:
①若![]() ,
,![]() ,则
,则![]() 的面积为____;
的面积为____;
②当![]() 的度数为____时,四边形
的度数为____时,四边形![]() 是菱形.
是菱形.
【答案】(1)见解析;(2)①![]() ;②30°
;②30°
【解析】
(1)由等腰三角形的性质得出∠B=∠C,∠B=∠BDO,证出OD∥AC,由已知条件得出∠C+∠CDF=90°,即可得出结论;
(2)解:①由AB是⊙O的直径,可得∠ADB=∠AEB=90°,即AD⊥BC由等腰三角形三线合一可得:BC=CD=![]() ,可证△ABE是等腰直角三角形,根据勾股定理可得:
,可证△ABE是等腰直角三角形,根据勾股定理可得:![]() ,代入数据可得:
,代入数据可得:![]() 故
故![]() 可得△BEC的面积,证得:△CBE∽△CDF,故
可得△BEC的面积,证得:△CBE∽△CDF,故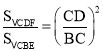 ,即可得出答案;
,即可得出答案;
②证出△ABC是等边三角形,得出∠ACB=60°,故∠CDF的度数,即可得出答案.
(1)证明:连接OD,∵AB=AC,OB=OD,
∴∠B=∠C,∠B=∠BDO,
∴∠C=∠BDO,
∴OD∥AC,
∵DF是⊙O的切线,
∴∠ODF=90°,
∴∠BDO+∠CDF=90°,
∴∠C+∠CDF=90°,
∴∠CFD=90°,
∴DF⊥AC;
(2)解:①∵连接AC,BE,
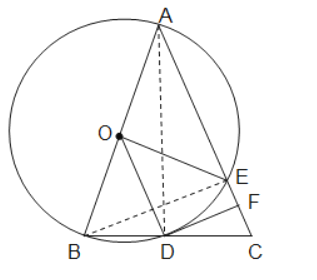
∵AB是⊙O的直径,
∴∠ADB=∠AEB=90°,
∴AD⊥BC
∵AB=AD=4,
∴BC=CD=![]() ,
,
在Rt△ABE中,∠AEB=90°,∠BAE=45°
∴∠ABE=90°-∠BAE=45°=∠BAE,
∴BE=AE
根据勾股定理可得![]() ,
,
即![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵DF⊥AC
∴∠DFE=∠DFC=90°
∵∠AEB=90°
∴∠AEB=∠DFE
∴BE∥DF,
∴△CBE∽△CDF
∴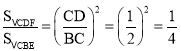
∴![]()
故答案为:![]()
②当四边形OECD是菱形时,OE∥DC
∴∠OEA=∠ACB
∵AB=AC,OA=OE
∴∠ABC=∠ACB,∠OAE=∠OEA
∴∠OAE=∠ABC=∠ACB
∴△ABC是等边三角形
∴∠ACB=60°
∴∠CDF=90°-∠DCF=90°-60°=30°
∴当∠CDF得度数为30°,四边形OECD是菱形
故答案为30°


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
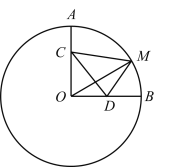
【题目】如图,在⊙O中,点A、点B在⊙O上,∠AOB=90°,OA=6,点C在OA上,且OC=2AC,点D是OB的中点,点M是劣弧AB上的动点,则CM+2DM的最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A、B两种新型节能台灯,已知B型节能台灯每盏进价比A型的多40元,且用3000元购进的A型节能台灯与用5000元购进的B型节能台灯的数量相同.
(1)求每盏A型节能台灯的进价是多少元?
(2)商场将购进A、B两型节能台灯100盏进行销售,A型节能台灯每盏的售价为90元,B型节能台灯每盏的售价为140元,且B型节能台灯的进货数量不超过A型节能台灯数量的2倍.应怎样进货才能使商场在销售完这批台灯时利最多?此时利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
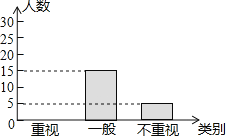
【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
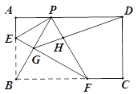
【题目】如图在矩形ABCD中,AB=6,AD=![]() ,点E在AB上,且AE=2,将该矩形沿EF折叠,使点B恰好落在AD边上的点P处,连接PB交EF于点G,连接PF、DG它们的交点为点H,则HD=______.
,点E在AB上,且AE=2,将该矩形沿EF折叠,使点B恰好落在AD边上的点P处,连接PB交EF于点G,连接PF、DG它们的交点为点H,则HD=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线x=1是二次函数y=ax2+bx+c(a,b,c是实数,且a≠0)的图象的对称轴,点A(x1,y1)和点B(x2,y2)为其图象上的两点,且y1<y2,( )
A.若x1<x2,则x1+x2﹣2<0B.若x1<x2,则x1+x2﹣2>0
C.若x1>x2,则a(x1+x2-2)>0D.若x1>x2,则a(x1+x2-2)<0
查看答案和解析>>
科目:初中数学 来源: 题型:
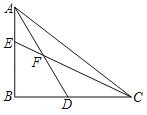
【题目】如图,在△ABC中,∠ABC=90°,D为BC的中点,点E在AB上,AD,CE交于点F,AE=EF=4,FC=9,则cos∠ACB的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日是世界读书日,设立的目的是推动更多的人去阅读和写作.为了解学生的课外阅读情况,对某校八年级1班“你最喜爱的课外阅读书目”进行调查(每名学生必须选一类且只能选一类阅读书目),并根据调查结果绘制成如图所示的两幅统计图(不完整).
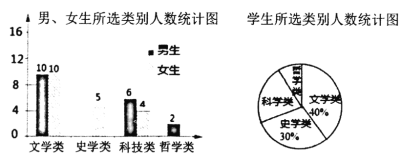
根据以上信息解决下列问题
(1)所抽查的学生中,选史学类的男生有______人,选哲学类的女生有______人;
(2)扇形统计图中“科学类”所对应扇形圆心角度数为_______°;
(3)若该校有2000名学生,请估计该校喜爱“科学类”的学生共有多少人?
(4)从所抽取的选“哲学类”的学生中,随机选取两名学生参加区级辩论赛,请用树状图或列表法求出所选取的两名学生恰好选中一个男生、一个女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com