
【题目】如图,四条直线l1:y1=![]() x,l2:y2=
x,l2:y2=![]() x,l3:y3=﹣
x,l3:y3=﹣![]() x,l4:y4=﹣
x,l4:y4=﹣![]() x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为________.
x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为________.
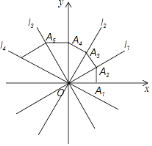
【答案】((![]() )2016,0)
)2016,0)
【解析】
先利用各直线的解析式得到x轴、l1、l2、y轴、l3、l4依次相交为30的角,各点的位置是每12个一循环,由于2017=168×12+1,则可判定点A2017在x轴的正半轴上,再规律得到OA2016=(![]() )2015,然后表示出点A2017坐标.
)2015,然后表示出点A2017坐标.
解:∵l1:y1=![]() x,l2:y2=
x,l2:y2=![]() x,l3:y3=-
x,l3:y3=-![]() x,l4:y4=-﹣
x,l4:y4=-﹣![]() x,
x,
∴x轴、l1、l2、y轴、l3、l4依次相交为30的角,
∵2017=168×12+1,
∴点A2017在x轴的正半轴上,
∵OA2=![]() =
=![]() ,
,
OA3=(![]() )2,
)2,
OA4=(![]() )3,
)3,
…
OA2017=(![]() )2016,
)2016,
∴点A2017坐标为((![]() )2016,0).
)2016,0).
故答案为((![]() )2016,0).
)2016,0).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2﹣2x﹣3的图象与x轴的交点为(﹣1,0)和(3,0),交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解.
根据以上方程与函数的关系,如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标,即可知方程x3+2x2﹣x﹣2=0的解.
佳佳为了解函数y=x3+2x2﹣x﹣2的图象,通过描点法画出函数的图象.
x | … | ﹣3 | ﹣ | ﹣2 | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| 2 | … |
y | … | ﹣8 | ﹣ | 0 |
| m | ﹣ | ﹣2 | ﹣ | 0 |
| 12 | … |
(1)直接写出m的值,并画出函数图象;
(2)根据表格和图象可知,方程的解有 个,分别为 ;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在![]() 点上正方
点上正方![]() 的
的![]() 处发出一球,羽毛球飞行的高度
处发出一球,羽毛球飞行的高度![]() 与水平距离
与水平距离![]() 之间满足函数表达式
之间满足函数表达式![]() .已知点
.已知点![]() 与球网的水平距离为
与球网的水平距离为![]() ,球网的高度为
,球网的高度为![]() .
.
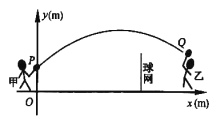
(1)当![]() 时,①求
时,①求![]() 的值.②通过计算判断此球能否过网.
的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到点![]() 的水平距离为
的水平距离为![]() ,离地面的高度为
,离地面的高度为![]() 的
的![]() 处时,乙扣球成功,求
处时,乙扣球成功,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
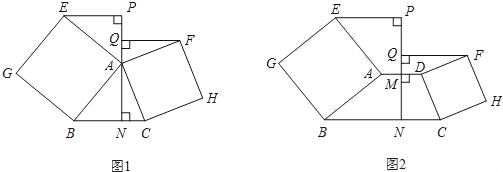
【题目】(1)已知:如图1,△ABC中,分别以AB、AC为一边向△ABC外作正方形ABGE和ACHF,直线AN⊥BC于N,若EP⊥AN于P,FQ⊥AN于Q.判断线段EP、FQ的数量关系,并证明;
(2)如图2,梯形ABCD中,AD∥BC,分别以两腰AB、CD为一边向梯形ABCD外作正方形ABGE和DCHF,线段AD的垂直平分线交线段AD于点M,交BC于点N,若EP⊥MN于P,FQ⊥MN于Q.(1)中结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2﹣2x+3用配方法化成y=a(x﹣h)2+k的形式是________,抛物线与x轴的交点坐标是________,抛物线与y轴的交点坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①对角线互相垂直且相等的平行四边形是正方形;
②平行四边形、矩形、等边三角形、正方形既是中心对称图形,也是轴对称图形;
③旋转和平移都不改变图形的形状和大小;
④底角是45°的等腰梯形,高是h,则腰长是![]() h;
h;
⑤一组对边平行,另一组对边相等的四边形是平行四边形.
以上正确的命题是( )
A. ①②③④ B. ①②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com