
分析 (1)首先化简a=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$,进一步化简代数式,代入求得答案即可;
(2)利用平方差公式分解因式,进一步计算交错约分得出答案即可;
(3)把每一项通分,进一步分解因式,交错约分得出答案即可.
解答 解:(1)∵a=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$,
∴$\frac{1-2a+{a}^{2}}{a-1}$-$\frac{\sqrt{{a}^{2}-2a+1}}{{a}^{2}-a}$
=$\frac{(a-1)^{2}}{a-1}-\frac{\sqrt{(a-1)^{2}}}{a(a-1)}$
=a-1-$\frac{1-a}{a(a-1)}$
=a-1+$\frac{1}{a}$
=2-$\sqrt{3}-1+\frac{1}{2-\sqrt{3}}$
=2-$\sqrt{3}-1+2+\sqrt{3}$
=3;
(2)(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{1{0}^{2}}$)
=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)(1-$\frac{1}{4}$)(1+$\frac{1}{4}$)…(1-$\frac{1}{10}$)(1+$\frac{1}{10}$)
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…×$\frac{9}{10}$×$\frac{11}{10}$
=$\frac{11}{20}$;
(3)∵4x4+1=4x4+4x2+1-4x2=(2x2+1)2-(2x)2=(2x2+1+2x)(2x2+1-2x)=[(x+1)2+x2][(x-1)2+x2],
∴$\frac{({2}^{4}+\frac{1}{4})({4}^{4}+\frac{1}{4})({6}^{4}+\frac{1}{4})({8}^{4}+\frac{1}{4})(1{0}^{4}+\frac{1}{4})}{({1}^{4}+\frac{1}{4})({3}^{4}+\frac{1}{4})({5}^{4}+\frac{1}{4})({7}^{4}+\frac{1}{4})({9}^{4}+\frac{1}{4})}$
=$\frac{\frac{4×{2}^{4}+1}{4}×\frac{4×{4}^{4}+1}{4}…\frac{4×1{0}^{4}+1}{4}}{\frac{4×{1}^{4}+1}{4}×\frac{4×{3}^{4}+1}{4}…\frac{4×{9}^{4}+1}{4}}$
=$\frac{(4×{2}^{4}+1)(4×{4}^{4}+1)…(4×1{0}^{4}+1)}{(4×{1}^{4}+1)(4×{3}^{4}+1)…(4×{9}^{4}+1)}$
=$\frac{({1}^{2}+{2}^{2})({2}^{2}+{3}^{2})({3}^{2}+{4}^{2})({4}^{2}+{5}^{2})…(1{0}^{2}+1{1}^{2})}{({0}^{2}+{1}^{2})({1}^{2}+{2}^{2})({2}^{2}+{3}^{2})({3}^{2}+{4}^{2})…({9}^{2}+1{0}^{2})}$
=$\frac{1{0}^{2}+1{1}^{2}}{{0}^{2}+{1}^{2}}$
=100+121
=221.
点评 此题考查二次根式的化简求值,因式分解的实际运用,掌握因式分解的方法是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq得,x2+(p+q)x+pq=(x+p)(x+q);利用这个式子可以将某些二次项系数是1的二次三项式分解因式,例如:将式子x2-x-6分解因式.这个式子的常数项-6=2×(-3),一次项系数-1=2+(-3),这个过程可用十字相乘的形式形象地表示:先分解常数项,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数.如图所示.这种分解二次三项式的方法叫“十字相乘法”,请同学们认真观察,分析理解后,解答下列问题.
阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq得,x2+(p+q)x+pq=(x+p)(x+q);利用这个式子可以将某些二次项系数是1的二次三项式分解因式,例如:将式子x2-x-6分解因式.这个式子的常数项-6=2×(-3),一次项系数-1=2+(-3),这个过程可用十字相乘的形式形象地表示:先分解常数项,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数.如图所示.这种分解二次三项式的方法叫“十字相乘法”,请同学们认真观察,分析理解后,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | (3)(4)(1)(2) | B. | (4)(3)(1)(2) | C. | (4)(3)(2)(1) | D. | (2)(4)(3)(1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
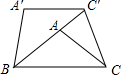 如图,将△ABC绕点B逆时针旋转40°,得到△A′B′C′,若点C′恰好落在边BA的延长线上,且A′C′∥BC,连接CC′,则∠ACC′=30度.
如图,将△ABC绕点B逆时针旋转40°,得到△A′B′C′,若点C′恰好落在边BA的延长线上,且A′C′∥BC,连接CC′,则∠ACC′=30度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$,$\sqrt{2}$,2 | B. | 9,16,25 | C. | 6,8,10 | D. | 5,12,13 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com