
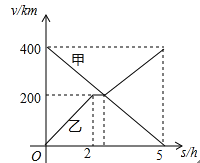
【题目】甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲,乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)乙车休息了 h;
(2)求乙车与甲车相遇后y乙与x的函数解析式,并写出自变量x的取值范围;
(3)当两车相距40km时,直接写出x的值.
【答案】(1)0.5;
(2)乙车与甲车相遇后y乙与x的函数解析式y乙=80x(2.5≤x≤5);
(3)x=2或x=![]() .
.
【解析】
(1)由待定系数法,可得y甲的解析式,根据函数值为200千米时,可得相应自变量的值,根据自变量的差,可得答案;
(2)由待定系数法,可得y乙的函数解析式;
(3)分类讨论,0≤x≤2.5,y甲减y乙等于40千米,2.5≤x≤5时,y乙减y甲等于40千米,即可得答案.
解:(1)设甲车行驶的函数解析式为y甲=kx+b,(k≠0的常数)
y甲=kx+b图象过点(0,400),(5,0),得
![]() ,解得
,解得![]() ,
,
甲车行驶的函数解析式为y甲=﹣80x+400,
当y=200时,x=2.5(h),
2.5﹣2=0.5(h),
(2)设乙车与甲车相遇后y乙与x的函数解析式y乙=kx+b,
y乙=kx+b图象过点(2.5,200),(5.400),得
![]() ,解得
,解得![]() ,
,
乙车与甲车相遇后y乙与x的函数解析式y乙=80x(2.5≤x≤5);
(3)设乙车与甲车相遇前y乙与x的函数解析式y乙=kx,图象过点(2.5,200),
解得k=80,
∴乙车与甲车相遇后y乙与x的函数解析式y乙=80x,
0≤x≤2.5,y甲减y乙等于40千米,
即400﹣80x﹣100x=40,解得 x=2;
2.5≤x≤5时,y乙减y甲等于40千米,
即2.5≤x≤5时,80x﹣(﹣80x+400)=40,解得x=![]() ,
,
综上所述:x=2或x=![]() .
.


科目:初中数学 来源: 题型:
【题目】某初中学校组织200位同学参加义务植树活动,每人植树的棵数在5至10之间.甲同学抽查了30位同学的植树情况,并将收集的数据进行了整理,绘制成统计表如下:(单位:棵)
每人植树情况 | 6 | 7 | 8 | 9 | 10 |
人数 | 3 | 6 | 3 | 11 | 6 |
人数/抽查总人数 | 0.1 | 0.2 | 0.1 | 0.4 | 0.2 |
根据以上材料回答下列问题:
(1)此表的最后两列中有一个错误的数据,这个错误的数据是________,正确的数据应该是________;
(2)表中30位同学植树情况的中位数是________棵,众数是________棵;
(3)并用该样本估计本次活动200位同学一共植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C′处,若∠ADB=46°,则∠DBE的度数为 °.
(2)小明手中有一张矩形纸片ABCD,AB=4,AD=9.
(画一画)
如图2,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为MN(点M,N分别在边AD,BC上),利用直尺和圆规画出折痕MN(不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);
(算一算)
如图3,点F在这张矩形纸片的边BC上,将纸片折叠,使FB落在射线FD上,折痕为GF,点A,B分别落在点A′,B′处,若AG=![]() ,求B′D的长;
,求B′D的长;
(验一验)
如图4,点K在这张矩形纸片的边AD上,DK=3,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点A′,B′处,小明认为B′I所在直线恰好经过点D,他的判断是否正确,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
请根据图表信息回答下列问题:
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)本次调查的样本为________,样本容量为_______;
(2)在频数分布表中,a=______,b=______,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校购买一批办公用品,有甲、乙两家超市可供选择:甲超市给予每件0.8元的优惠价格,乙商超市的优惠条件如图象所示.

(1)分别求出在两家超市购买费用 y(元)与购买数量x(件)的函数关系式;
(2)若你是学校采购员,应如何选择才能更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,我们在“格点”直角坐标系上可以看到:要找![]() 或
或![]() 的长度,可以转化为求
的长度,可以转化为求![]() 或
或![]() 的斜边长.
的斜边长.

例如:从坐标系中发现:![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以由勾股定理可得:
,所以由勾股定理可得:![]() .
.
(1)在图①中请用上面的方法求线段![]() 的长:
的长:![]() ______;在图②中:设
______;在图②中:设![]() ,
,![]() ,试用
,试用![]() ,
,![]() ,
,![]() ,
,![]() 表示:
表示:![]() ______.
______.
(2)试用(1)中得出的结论解决如下题目:已知:![]() ,
,![]() ,
,![]() 为
为![]() 轴上的点,且使得
轴上的点,且使得![]() 为等腰三角形,请求出
为等腰三角形,请求出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形的周长为32cm,一个内角的度数是60°,则两条对角线的长分别是( )
A. 8cm和4![]() cm B. 4cm和8
cm B. 4cm和8![]() cm C. 8cm和8
cm C. 8cm和8![]() cm D. 4cm和4
cm D. 4cm和4![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】食品加工是一种专业技术,就是把原料经过人为处理形成一种新形式的可直接食用的产品,这个过程就是食品加工.比如用小麦经过碾磨、筛选、加料搅拌、成型烘干,成为饼干,就是属于食品加工的过程.下表给出了甲、乙、丙三种原料中的维生素A、B的含量(单位:g/kg).
原料甲 | 原料乙 | 原料丙 | |
维生素A的含量 | 4 | 6 | 4 |
维生素B的含量 | 8 | 2 | 4 |
将甲、乙、丙三种原料共100kg混合制成一种新食品,其中原料甲xkg,原料乙ykg.
(1)这种新食品中,原料丙的含量__________kg,维生素B的含量__________g;(用含![]() 、
、![]() 的式子表示)
的式子表示)
(2)若这种新食品中,维生素A的含量至少为440g,维生素B的含量至少为480g,请你证明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角板中的两个直角顶点重合在一起,即按如图所示的方式叠放在一起,其中∠A=60°,∠B=30,∠D=45°.
(1)若∠BCD=45°,求∠ACE的度数.
(2)若∠ACE=150°,求∠BCD的度数.
(3)由(1)、(2)猜想∠ACE与∠BCD存在什么样的数量关系并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com