
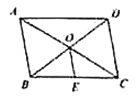
【题目】如图,![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 中点,若
中点,若![]() 的周长为28,
的周长为28,![]() ,则
,则![]() 的周长为( )
的周长为( )
A.12B.17C.19D.24
【答案】A
【解析】
由四边形ABCD是平行四边形,根据平行四边形的性质可得OB=OD,再由E是CD中点,即可得BE=![]() BC,OE是△BCD的中位线,由三角形的中位线定理可得OE=
BC,OE是△BCD的中位线,由三角形的中位线定理可得OE=![]() AB, 再由ABCD的周长为28,BD=10, 即可求得AB+BC=14,BO=5,由此可得BE+OE=7, 再由△OBE的周长为=BE+OE+BO即可求得△OBE的周长.
AB, 再由ABCD的周长为28,BD=10, 即可求得AB+BC=14,BO=5,由此可得BE+OE=7, 再由△OBE的周长为=BE+OE+BO即可求得△OBE的周长.
∵四边形ABCD是平行四边形,
∴O是BD中点, OB=OD,
又∵E是CD中点,
∴BE=![]() BC,OE是△BCD的中位线,
BC,OE是△BCD的中位线,
∴OE=![]() AB,
AB,
∵ABCD的周长为28,BD=10,
∴AB+BC=14,
∴BE+OE=7,BO=5
∴△OBE的周长为=BE+OE+BO=7+5=12.
故选A.


科目:初中数学 来源: 题型:
【题目】某草莓种植大户,今年从草莓上市到销售完需要20天,售价为15元/千克,成本y(元/千克)与第x天成一次函数关系,当x=10时,y=7,当x=15时,y=6.5.
(1)求成本y(元/千克)与第x天的函数关系式并写出自变量x的取值范围;
(2)求第几天每千克的利润w(元)最大?最大利润是多少?(利润=售价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
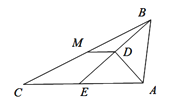
【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
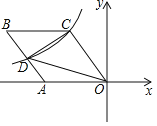
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
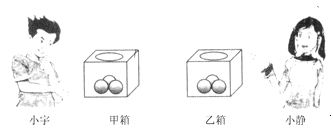
【题目】如图,有6个质地和大小均相同的球,每个球只标有一个数字,将标有3,4,5的三个球放入甲箱中,标有4,5,6的三个球放入乙箱中.
(1)小宇从甲箱中随机模出一个球,求“摸出标有数字是3的球”的概率;
(2)小宇从甲箱中、小静从乙箱中各自随机摸出一个球,若小宇所摸球上的数字比小静所摸球上的数字大1,则称小宇“略胜一筹”.请你用列表法(或画树状图)求小宇“略胜一筹”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.

(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
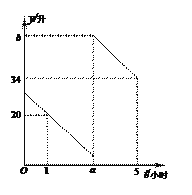
【题目】张师傅驾驶某种型号轿车从甲地去乙地,该种型号轿车每百公里油耗为10升(每行驶100公里需消耗10升汽油).途中在加油站加了一次油,加油前,根据仪表盘显示,油箱中还剩4升汽油.假设加油前轿车以80公里/小时的速度匀速行驶,加油后轿车以90公里/小时的速度匀速行驶(不计加油时间),已知油箱中剩余油量y(升)与行驶时间t(小时)之间的函数关系如图所示.
(1) 加油前,该轿车每小时消耗汔油 升;加油后,该轿车每小时消耗汔油 升;
(2)求加油前油箱剩余油量y(升)与行驶时间t(小时)之间的函数表达式;
(3)求张师傅在加油站加了多少升汽油.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com