
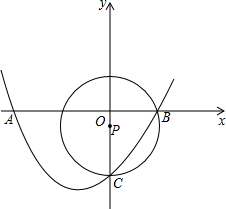
 “—÷™£∫»ÁÕº£¨≈◊ŒÔœþy=ax2+bx+c£®a°Ÿ0£©æ≠π˝X÷·…œµƒ¡Ωµ„A£®x1£¨0£©°¢B£®x2£¨0£©∫Õy÷·…œµƒµ„C£®0£¨-1.5£©£¨°—Pµƒ‘≤–ƒP‘⁄y÷·…œ£¨«“æ≠π˝B°¢C¡Ωµ„£¨»Ùb=
“—÷™£∫»ÁÕº£¨≈◊ŒÔœþy=ax2+bx+c£®a°Ÿ0£©æ≠π˝X÷·…œµƒ¡Ωµ„A£®x1£¨0£©°¢B£®x2£¨0£©∫Õy÷·…œµƒµ„C£®0£¨-1.5£©£¨°—Pµƒ‘≤–ƒP‘⁄y÷·…œ£¨«“æ≠π˝B°¢C¡Ωµ„£¨»Ùb=| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
| b |
| 2a |
| ||
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |


 “ª≈µ È“µ ÓºŸ◊˜“µøÏ¿÷ºŸ∆⁄‘∆ƒœ√¿ ı≥ˆ∞Ê…Áœµ¡–¥∞∏
“ª≈µ È“µ ÓºŸ◊˜“µøÏ¿÷ºŸ∆⁄‘∆ƒœ√¿ ı≥ˆ∞Ê…Áœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
 »ÁÕº£¨‘⁄?ABCD÷–£¨E°¢F∑÷± «AD°¢AB…œµƒµ„£¨«“BE=DF£¨BEΩªDF”⁄P°¢ΩªCDµƒ—”≥§œþ”⁄Q£¨«Û÷§£∫CD£∫CQ=PD£∫PQ£Æ
»ÁÕº£¨‘⁄?ABCD÷–£¨E°¢F∑÷± «AD°¢AB…œµƒµ„£¨«“BE=DF£¨BEΩªDF”⁄P°¢ΩªCDµƒ—”≥§œþ”⁄Q£¨«Û÷§£∫CD£∫CQ=PD£∫PQ£Æ≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
| 2 |
| 3 |
| 11 |
| 12 |
| 14 |
| 15 |
| 3 |
| 7 |
| 7 |
| 4 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
| 1 |
| 2x+6 |
| 1 |
| 3-x |
| x |
| 2(x2-9) |
| a+2 |
| a2-2a |
| 8 |
| 4-a2 |
| a-2 |
| a |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
 »ÁÕº£¨AC=AE£¨AB=AD£¨°œ1=°œ2£Æ
»ÁÕº£¨AC=AE£¨AB=AD£¨°œ1=°œ2£Æ≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
 »ÁÕº£¨“—÷™Àƒ±þ–ŒABCDŒ™’˝∑Ω–Œ£¨E£¨FŒ™AB°¢CDµƒ÷–µ„£¨AD=2£¨°˜AGF «”…°˜ADF’€µ˛∂¯¿¥µƒ£¨¡¨Ω”GI£¨ πµ√GI°ÕAB£Æ
»ÁÕº£¨“—÷™Àƒ±þ–ŒABCDŒ™’˝∑Ω–Œ£¨E£¨FŒ™AB°¢CDµƒ÷–µ„£¨AD=2£¨°˜AGF «”…°˜ADF’€µ˛∂¯¿¥µƒ£¨¡¨Ω”GI£¨ πµ√GI°ÕAB£Æ≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com