
分析 该题需要分类讨论:射线OA在∠BOD的内部和外部两种情况,然后根据角平分线的定义进行解答.
解答  解:①如图1,∵∠AOB=50°,∠BOD=3∠AOB,
解:①如图1,∵∠AOB=50°,∠BOD=3∠AOB,
∴∠BOD=150°.
∴∠AOD=150°-50°=100°.
∵OM平分∠AOB,ON平分∠AOD,
∴∠AOM=∠$\frac{1}{2}$AOB=25°,∠AON=∠$\frac{1}{2}$AOD=65°,
∴∠MON=∠AON+∠AOM=75°;
②如图2,∵∠AOB=50°,∠BOD=3∠AOB,
∴∠BOD=150°.
∴∠AOD=360°-(150°+50°)=160°.
∵OM平分∠AOB,ON平分∠AOD,
∴∠BOM=∠$\frac{1}{2}$AOB=25°,∠AON=∠$\frac{1}{2}$AOD=80°,
∴∠MON=∠AOM+∠AON=80°+25°=105°;
综上所述,∠MON的度数是75°或105°.
点评 本题考查了角平分线的定义.根据角平分线定义得出所求角与已知角的关系转化求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
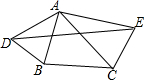 如图,△ABC中,AB=6,AC=8,分别以AB、AC为一边向外作等腰△ADB和等腰△ACE,AD=AB,AE=AC,且∠DAB=∠EAC=x,∠BAC=y(其中2x+y<180°).
如图,△ABC中,AB=6,AC=8,分别以AB、AC为一边向外作等腰△ADB和等腰△ACE,AD=AB,AE=AC,且∠DAB=∠EAC=x,∠BAC=y(其中2x+y<180°).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
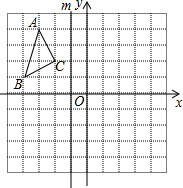 如图所示的正方形网格中,每个小正方形的边长为1,△ABC的三个顶点都在格点上.
如图所示的正方形网格中,每个小正方形的边长为1,△ABC的三个顶点都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18x+32=20x-8 | B. | 18x+32=20x+8 | C. | 18x-32=20x-8 | D. | 18x-32=20x+8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
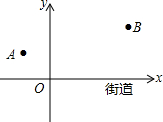 去年“双11”购物节的快递量暴增,某快递公司要在街道旁设立一个派送还点,向A、B两居民区投送快递,派送点应该设在什么地方,才能使它到A、B的距离之和最短?快递员根据实际情况,以街道为x轴,建立了如图所示的平面直角坐标系,测得坐标A(-2,2)、B(6,4),则派送点的坐标是($\frac{2}{3}$,0).
去年“双11”购物节的快递量暴增,某快递公司要在街道旁设立一个派送还点,向A、B两居民区投送快递,派送点应该设在什么地方,才能使它到A、B的距离之和最短?快递员根据实际情况,以街道为x轴,建立了如图所示的平面直角坐标系,测得坐标A(-2,2)、B(6,4),则派送点的坐标是($\frac{2}{3}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com