
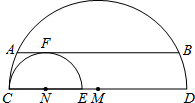
 如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设
如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设 |
| CD |
 |
| CE |
| 1 |
| 2 |
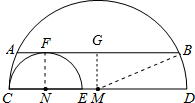 设⊙M,⊙N的半径分别为R,r,
设⊙M,⊙N的半径分别为R,r,| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点C为线段AB上一点,D为AC的中点,点E为线段BD的中点.
如图,点C为线段AB上一点,D为AC的中点,点E为线段BD的中点.| 1 |
| 2 |
| BC |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知正△ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG=x,设△EFG的面积为y,则y关于x的函数关系式为( )
如图,已知正△ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG=x,设△EFG的面积为y,则y关于x的函数关系式为( )A、-
| ||||||||
B、-
| ||||||||
C、
| ||||||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
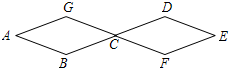 如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由A点开始按ABCDEF的顺序按菱形的边循环运动,行走2015厘米后停下,则这只蚂蚁停在( )
如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由A点开始按ABCDEF的顺序按菱形的边循环运动,行走2015厘米后停下,则这只蚂蚁停在( )| A、B点 | B、C点 | C、G点 | D、E点 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 老师布置了一道考题:如图所示,点M、N分别在正△ABC的边BC、CA上,且BM=CN,AM交BN于点Q.
老师布置了一道考题:如图所示,点M、N分别在正△ABC的边BC、CA上,且BM=CN,AM交BN于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com