
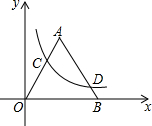
 如图,△AOB是边长为a的等边三角形,OC=3BD,求反比例函数y=
如图,△AOB是边长为a的等边三角形,OC=3BD,求反比例函数y=| k |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
3
| ||
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
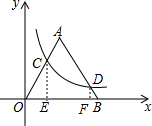 解:作CE⊥x轴于E,作DF⊥x轴于F,如图,
解:作CE⊥x轴于E,作DF⊥x轴于F,如图,| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
3
| ||
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| k |
| x |
| 3 |
| 2 |
3
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 5 |
9
| ||
| 4 |
| 1 |
| 25 |
9
| ||
| 100 |
| k |
| x |


科目:初中数学 来源: 题型:
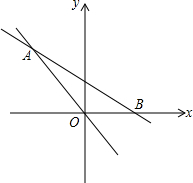 已知,正比例函数y=k1x和一次函数y=k2x+br的图象如图所示,它们的交点A(-3,4),且OB=
已知,正比例函数y=k1x和一次函数y=k2x+br的图象如图所示,它们的交点A(-3,4),且OB=| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在六边形ABCDEF中,所有角都相等.
如图,在六边形ABCDEF中,所有角都相等.查看答案和解析>>
科目:初中数学 来源: 题型:
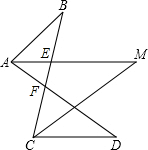 (1)如图所示,已知∠B=32°,∠D=38°,AM,CM分别平分∠BAD和∠BCD,求∠M的度数.
(1)如图所示,已知∠B=32°,∠D=38°,AM,CM分别平分∠BAD和∠BCD,求∠M的度数.查看答案和解析>>
科目:初中数学 来源: 题型:
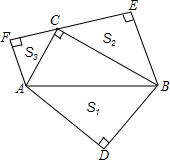 如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC、AC为斜边向外作等腰直角三角形,设所作的△ABD、△BCE、△ACF的面积分别为S1、S2、S3,求证:S1=S2+S3.
如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC、AC为斜边向外作等腰直角三角形,设所作的△ABD、△BCE、△ACF的面积分别为S1、S2、S3,求证:S1=S2+S3.查看答案和解析>>
科目:初中数学 来源: 题型:
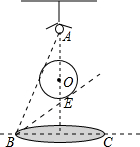 如图,有一悬挂的球,球心为点O,球正上方A处有一小灯泡,球在桌面上投下的阴影是一个圆,其直径BC=30cm,在B处看球,最大仰角是60°,最小仰角是30°,求球心O到桌面的距离.
如图,有一悬挂的球,球心为点O,球正上方A处有一小灯泡,球在桌面上投下的阴影是一个圆,其直径BC=30cm,在B处看球,最大仰角是60°,最小仰角是30°,求球心O到桌面的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com