
【题目】如图,长方形纸片ABCD,点G在AB边上,点H在BC边上,连接GH,将∠CHG对折,点C落在直线HG上的点C′处,点D落在点D′处,得到折痕FH,C′D′与AD边交于点E
(1)如果∠CHF=80°,那么∠BHG的度数是多少?
(2)如果∠DFH=110°,那么∠D′FE的度数是多少?

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() ,直线
,直线![]() 与x轴、y轴分别交于B、C两点,并与直线
与x轴、y轴分别交于B、C两点,并与直线![]() 相交于点D,若
相交于点D,若![]() .
.
![]() 求点D的坐标;
求点D的坐标;
![]() 求出四边形AOCD的面积;
求出四边形AOCD的面积;
![]() 若E为x轴上一点,且
若E为x轴上一点,且![]() 为等腰三角形,写出点E的坐标
为等腰三角形,写出点E的坐标![]() 直接写出答案
直接写出答案![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某河道A,B两个码头之间有客轮和货轮通行![]() 一天,客轮从A码头匀速行驶到B码头,同时货轮从
一天,客轮从A码头匀速行驶到B码头,同时货轮从
B码头出发,运送一批建材匀速行驶到A码头![]() 两船距B码头的距离
两船距B码头的距离![]() 千米
千米![]() 与行驶时间
与行驶时间![]() 分
分![]() 之间的函数关系
之间的函数关系
如图所示![]() 请根据图象解决下列问题:
请根据图象解决下列问题:
![]() 分别求客轮和货轮距B码头的距离
分别求客轮和货轮距B码头的距离![]() 千米
千米![]() 、
、![]() 千米
千米![]() 与
与![]() 分
分![]() 之间的函数关系式;
之间的函数关系式;
![]() 求点M的坐标,并写出该点坐标表示的实际意义.
求点M的坐标,并写出该点坐标表示的实际意义.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=4(单位长度),CD=6(单位长度),点A在数轴上表示的数是-16,点C在数轴上表示的数是18
![]()
(1) 点B在数轴上表示的数是多少,点D在数轴上表示的数是多少,线段AD等于 多少;
(2) 若线段AB以4个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动,设运动时间为t秒
①若BC=6(单位长度),求t的值
②当0<t<5时,设M为AC中点,N为BD中点,求线段MN的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买一批单价为20元的日用品,如果以单价30元销售,那么半月内可以售出400件.据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高一元,销售量相应减少20件.如何提高销售价,才能在半月内获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm,点E、F、G分别从A、B、C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E、F、G运动的时间为t(单位:s).
(1)当t=s时,四边形EBFB′为正方形;
(2)若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;
(3)是否存在实数t,使得点B′与点O重合?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰三角形ABC中,AB=AC=4,BC=7.如图2,在底边BC上取一点D,连结AD,使得∠DAC=∠ACD.如图3,将△ACD沿着AD所在直线折叠,使得点C落在点E处,连结BE,得到四边形ABED.则BE的长是( ) 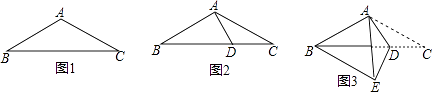
A.4
B.![]()
C.3 ![]()
D.2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com