
分析 设t=$\frac{x-1}{x+3}$,则原方程转化为关于t的一元二次方程,通过解该方程可以求得t的值,然后解关于x的分式方程.
解答 解:设t=$\frac{x-1}{x+3}$,则
t2-4t+1=0,
解得t=2±$\sqrt{3}$.
当t=2+$\sqrt{3}$时,
$\frac{x-1}{x+3}$=2+$\sqrt{3}$,即x=-$\frac{7+3\sqrt{3}}{\sqrt{3}+1}$
经检验x=-$\frac{7+3\sqrt{3}}{\sqrt{3}+1}$是原方程的根.
当$\frac{x-1}{x+3}$=2-$\sqrt{3}$,即x=$\frac{-7+3\sqrt{3}}{1-\sqrt{3}}$.
经检验x=$\frac{-7+3\sqrt{3}}{1-\sqrt{3}}$是原方程的根.
所以-$\frac{7+3\sqrt{3}}{\sqrt{3}+1}$×$\frac{-7+3\sqrt{3}}{1-\sqrt{3}}$=-$\frac{21}{2}$.
故答案是:-$\frac{21}{2}$.
点评 本题考查了换元法解分式方程.用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化,注意求出方程解后要验根.


科目:初中数学 来源: 题型:解答题
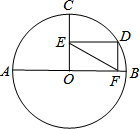 如图,⊙O的半径OC⊥AB,D为$\widehat{BC}$上一点,DE⊥OC,DF⊥AB,垂足分别为E、F,EF=3,求直径AB的长.
如图,⊙O的半径OC⊥AB,D为$\widehat{BC}$上一点,DE⊥OC,DF⊥AB,垂足分别为E、F,EF=3,求直径AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
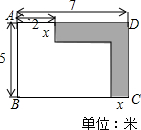 如图所示,客厅的地面是矩形ABCD,在它的一角摆放宽度相等的一张“7”字形的沙发,供会客用,要求摆放沙发后客厅地面的剩余面积为26平方米.若设沙发的宽度为x米,求x的值.
如图所示,客厅的地面是矩形ABCD,在它的一角摆放宽度相等的一张“7”字形的沙发,供会客用,要求摆放沙发后客厅地面的剩余面积为26平方米.若设沙发的宽度为x米,求x的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com