
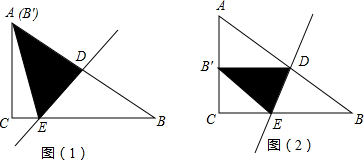
 解:(1)如图1,
解:(1)如图1,| 25 |
| 4 |
| 25 |
| 4 |
| 1 |
| 2 |
| 55 |
| 16 |
| 55 |
| 16 |


科目:初中数学 来源: 题型:
 如图,已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果AB=AC,∠FDE=∠B,BD=2,CD=3,CE=4,AE=1,那么AF的长为( )
如图,已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果AB=AC,∠FDE=∠B,BD=2,CD=3,CE=4,AE=1,那么AF的长为( )| A、3.5 | B、4 | C、4.5 | D、5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 勐海茶树王是西双版内众多古树之一,至今已有1800年的历史,茶树王于2012年10月“仙逝”.小刚曾经通过测量计算过茶树王的高度,他测量的方法是:如图,从点B沿水平线方向走到点D测得BD=17m,再用高为1.5m的测角仪CD,测得树顶的仰角为60°.请你根据以上数据计算茶树王AB的高度.(结果保留整数,
勐海茶树王是西双版内众多古树之一,至今已有1800年的历史,茶树王于2012年10月“仙逝”.小刚曾经通过测量计算过茶树王的高度,他测量的方法是:如图,从点B沿水平线方向走到点D测得BD=17m,再用高为1.5m的测角仪CD,测得树顶的仰角为60°.请你根据以上数据计算茶树王AB的高度.(结果保留整数,| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,△ABP和△CDP是两个全等的等边三角形,且AP⊥PD,有以下四个结论:
如图所示,△ABP和△CDP是两个全等的等边三角形,且AP⊥PD,有以下四个结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com