
【题目】问题提出:在矩形ABCD中,AB=6,BC=4,点E、F分别为边AD、BC上的点,且AE=1;BF=2.
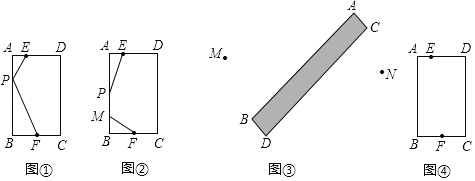
(1)如图①,P为边AB上一动点,连接EP、PF,则EP+PF的最小值为_____;
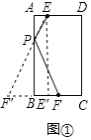
(2)如图②,P、M是AB边上两动点,且PM=2,现要求计算出EP、PM、MF和的最小值.九年级一班某兴趣小组通过讨论得出一个解决方法:在DA的延长线上取一点E',使AE'=AE,再过点E'作AB的平行线E'C,在E'C上E”的下方取点M,使E'M'=2,连接M'F,则与AB边的交点即为M,再在边AB上点M的上方取P点,且PM=2,此时EP+PM+MF的值最小.但他们不确定此方法是否可行,便去请教数学田老师,田老师高兴地说:“你们的做法是有道理的”.现在请你根据叙述作出草图并计算出EP+PM+MF的最小值;
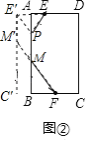
问题解决:(3)聪聪的爸爸是供电公司的线路设计师,公司准备架设一条经过农田区的输电线路,为M、N两个村同时输电.如图所示,农田区两侧AB与CD平行,且农田区宽为0.5千米,M村到AB的距离为2千米,N村到CD的距离为1千米,M、N所在的直线与AB所夹锐角恰好为45°,根据架线要求,在农田区内的线路要与AB垂直.请你帮助聪聪的爸爸设计出最短的线路图,并计算出最短线路的长度.(要求:写出计算过程,结果保留根号)
【答案】(1)![]() ;(2)EP+PM+MF的最小值是7;(3)
;(2)EP+PM+MF的最小值是7;(3)![]() km
km
【解析】
(1)利用轴对称方法求最短路线,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 或作点
或作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,则
,则![]() 即为最小值;
即为最小值;
(2)由于PM是定值,可以通过平移点的方式将问题转化为问题一,再通过对称求最短路线;
(3)由于农田的宽度一定,故可将M点延AB的垂直方向移动农田的宽度到![]() ,将问题转化为两点之间线段最短问题即可,作
,将问题转化为两点之间线段最短问题即可,作![]() ,并在
,并在![]() 上截取
上截取![]() (农田的宽度),连接
(农田的宽度),连接![]() 交
交![]() 于
于![]() ,作
,作![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 即为最短路线.
即为最短路线.
解:(1)如图①,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
![]() 矩形
矩形![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
当![]() ,
,![]() ,
,![]() 三点共线时,
三点共线时,![]() 最小,即
最小,即![]() 最小;
最小;
由勾股定理得:![]() ,
,
故答案为![]() ;
;
(2)如图②,延长![]() 至
至![]() ,使
,使![]() ,在
,在![]() 下方作
下方作![]() ,在
,在![]() 上截取
上截取![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,在
,在![]() 上截取
上截取![]() ,连接
,连接![]() ,
,![]() ,
,
![]() 矩形
矩形![]()
![]() ,即
,即![]() ,
,
![]()
![]()
![]() ,
,![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
![]() 为最小值,
为最小值,
即![]() 为最小值.
为最小值.
(3)如图③,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,
,
在![]() 上截取
上截取![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
![]() ,
,![]()
![]() ,
,
![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
由题意知,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
在![]() △
△![]() 中,
中,![]() ,
,
![]()
![]() 最短线路长度为
最短线路长度为![]() .
.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】小明从家步行到校车站台,等候坐校车去学校,图中的折线表示这一过程中小明的路程S(km)与所花时间t(min)间的函数关系;下列说法:①他步行了1km到校车站台;②他步行的速度是100m/min;③他在校车站台等了6min;④校车运行的速度是200m/min;其中正确的个数是( )个.
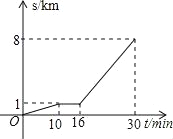
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为开展“大阅读”活动,购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格少5元.已知学校用12000元购买的文学类图书的本数与用9000元购买的科普类图书的本数相等,求学校购买的科普图书和文学类图书平均每本的价格各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
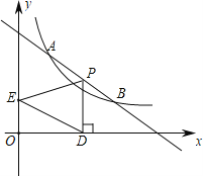
【题目】如图,直线y1=k1x+b与双曲线![]() 在第一象限内交于A、B两点,已知A(1,m),B(2,1).
在第一象限内交于A、B两点,已知A(1,m),B(2,1).
(1)直接写出不等式y2>y1的解集;
(2)求直线AB的解析式;
(3)设点P是线段AB上的一个动点,过点P作PD⊥x轴于点D,E是y轴上一点,求△PED的面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区教育系统为了更好地宣传扫黑除恶专项斗争,印制了应知应会手册,该区教育局想了解教师对扫黑除恶专项斗争应知应会知识掌握程度,抽取了部分教师进行了测试,并将测试成绩绘制成下面两幅统计图,请根据统计图中提供的信息,回答下面问题:
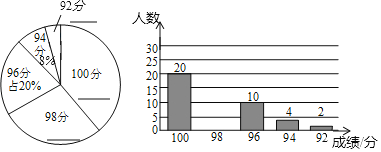
(1)计算样本中,成绩为98分的教师有 人,并补全两个统计图;
(2)样本中,测试成绩的众数是 ,中位数是 ;
(3)若该区共有教师6880名,根据此次成绩估计该区大约有多少名教师已全部掌握扫黑除恶专项斗争应知应会知识?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式![]() 的实数x的所有取值的全体叫做闭区间,表示为
的实数x的所有取值的全体叫做闭区间,表示为![]() 对于一个函数,如果它的自变量x与函数值y满足:当
对于一个函数,如果它的自变量x与函数值y满足:当![]() ,我们就称此函数是闭区间
,我们就称此函数是闭区间![]() 上的“闭函数”.
上的“闭函数”.
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此函数的解析式;
上的“闭函数”,求此函数的解析式;
(3)若函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求实数a,b的值.
上的“闭函数”,求实数a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
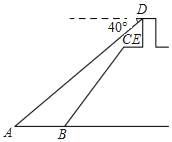
【题目】如图,小明站在江边某瞭望台DE的顶端D处,测得江面上的渔船A的俯角为40°.若瞭望台DE垂直于江面,它的高度为3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米.
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,cot40°≈1.19)
(1)求瞭望台DE的顶端D到江面AB的距离;
(2)求渔船A到迎水坡BC的底端B的距离.(结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一前夕某幼儿园园长到厂家选购A、B两种品牌的儿童服装每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍,求A、B两种品牌服装每套进价分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:所有正整数在进行某种规定步骤的运算后,会得到一个恒定不变的数,我们把这个恒定不变的数叫做稳定数.规定求三位数的稳定数的运算步骤是:任意三位数A=![]() (百位与个位不相同),将这个数逆置后得A1=
(百位与个位不相同),将这个数逆置后得A1=![]() ,A与A1中较大的数减去较小的数得到一个数B,再将B进行一次逆置得B1(若B为两位数则交换十位与个位逆置),将B1与B相加得C,C就是该三位数A的稳定数,记作
,A与A1中较大的数减去较小的数得到一个数B,再将B进行一次逆置得B1(若B为两位数则交换十位与个位逆置),将B1与B相加得C,C就是该三位数A的稳定数,记作![]() .
.
材料二:当两个三位数的稳定数相同时,这两个三位数的百位数字与个位数字之差的绝对值或者都大于1,或者都等于1.
(1)求352的稳定数是 ;百位与个位相差2的三位数,它的稳定数是 .
(2)现有S=301+10p,T=100m+40+n(1≤p≤9,1≤m≤9,1≤n≤9,p,m,n均是整数),其中T是偶数,若![]() ,3p+m+n=20,|p-n|=1,
,3p+m+n=20,|p-n|=1,![]() ,请求出
,请求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com