练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．比较下列各组中两个代数式的大小
    （1）x2+5x+6与2x2+5x+9；
    （2）（x-3）2与（x一2）（x-4）；
    （3）当x＞1时，x3与x2-x+1；
    （4）x2+y2+1与2（x+y-1）．

    分析 首先把两个代数式作差，再进一步利用配方法和非负数的性质得出答案即可．

    解答 解：（1）∵2x2+5x+9-（x2+5x+6）=x2+3＞0，
    ∴x2+5x+6＜2x2+5x+9．
    （2）∵（x-3）2-（x-2）（x-4）=x2-6x+9-（x2-6x+8）=1＞0，
    ∴（x-3）2＞（x-2）（x-4）；
    （3）∵x3-x2+x-1=x2（x-1）+（x-1）=（x-1）（x2+1）＞0，
    ∴x3＞x2-x+1；
    （4）∵x2+y2+1-2（x+y-1）=x2-2x+1+y2-2y+1+1=（x-1）2+（y-1）2+1＞0，
    ∴x2+y2+1＞2（x+y-1）．

    点评 此题考查因式分解的实际运用，非负数的性质，利用作差法比较大小，是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．一元二次方程x2+2=0的根的情况是（　　）
    A．有两个不相等的实数根B．有两个相等的实数根
    C．没有实数根D．只有一个实数根

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

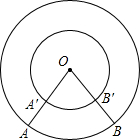    15．如图，两个同心圆的圆心为点O，A，B是最大圆上的两点，OA交小圆于点A′，OB交小圆于点B′，那么（　　）
    A．$\widehat{AB}$=$\widehat{A′B′}$B．$\widehat{AB}$＞$\widehat{A′B′}$
    C．$\widehat{AB}$的度数等于$\widehat{A′B′}$的度数D．$\widehat{AB}$的长度等于$\widehat{A′B′}$的长度

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．根据下列语句，设适当的未知数，列出二元一次方程（组）：
    （1）甲数的2倍与乙数的$\frac{1}{2}$的差等于48的$\frac{1}{3}$；
    （2）某学校招收八年级学生292人，其中男生人数比女生人数多35人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

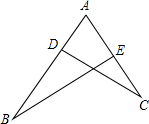    19．如图，点D在AB上，点E在AC上，且AD=$\frac{1}{3}$AC，AE=$\frac{1}{3}$AB．
    求证：△ABE∽△ACD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．把下列各式分解因式：
    （1）ax+ay；                   
    （2）3mx-6my；                                
    （3）8m2n+2mn；
    （4）12xyz-9x2y2；            
    （5）2a（y-z）-3b（z-y）；                    
    （6）p（a2+b2）-q（a2+b2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．计算：
    （1）32-17+（-23）；
    （2）（-2）+4$\frac{1}{4}$+2.75+（-3）；
    （3）（-3）×（-3$\frac{6}{7}$）+（-5）×（-3$\frac{6}{7}$）+8×（-3$\frac{6}{7}$）；
    （4）-14-3×[2-（-3）2]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知点A、B的坐标分别为（2，2）、（5，1），试在x轴上找一点C，使△ABC为直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．在数轴上，表示数m与n的点之间的距离可以表示为|m-n|．例如：在数轴上，表示数-3与2的点之间的距离是5=|-3-2|，表示数-4与-1的点之间的距离是3=|-4-（-1）|．利用上述结论解决如下问题：
    若点C、D为数轴上的两个动点，点C表示的数是c，点D表示的数是d，且|c-d|=4（c＞d），点Q表示的数为-1，当C、D、Q三点中的某一点是另两个点组成的线段的中点时，求c、d的值．

    查看答案和解析>>

    同步练习册答案