
分析 (1)利用待定系数法即可求得双曲线的解析式,进而求得B的坐标,然后根据待定系数法即可求得直线的解析式;
(2)一次函数的图象在反比例函数的图象的下边的自变量的取值范围.
解答 解:把A(-4,2)代入y2=$\frac{m}{x}$得:m=-8,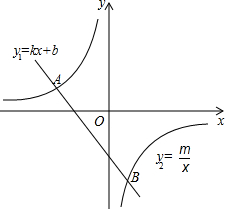
则反比例函数的解析式是:y2=-$\frac{8}{x}$;
把y=-4代入y2=-$\frac{8}{x}$,得:x=n=2,
则B的坐标是(2,-4).
把A、B坐标代入y1=kx+b,
$\left\{\begin{array}{l}{-4k+b=2}\\{2k+b=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=-2}\end{array}\right.$,
则一次函数的解析式为y=-x-2;
(2)∵A(-4,2)、B(2,-4),
∴y1<y2的x的取值范围是-4<x<0或x>2.
点评 本题综合考查一次函数与反比例函数的图象与性质,同时考查用待定系数法求函数解析式.本题需要注意无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;需注意反比例函数的自变量不能取0.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2tan60° | B. | $\sqrt{8}$ | C. | $\root{3}{16}$ | D. | π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
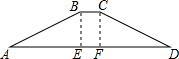 如图,为消除淮河灾害,某市水利部门修建了横断面是梯形的淮河大坝,坝顶宽6米,坝高BE=CF=20米,斜坡AB的坡角∠A=30°,斜坡CD的坡度i=1:3,(坡度是指坡面的铅直高度与水平宽度的比).求坝底AD的宽.(结果保留整数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,为消除淮河灾害,某市水利部门修建了横断面是梯形的淮河大坝,坝顶宽6米,坝高BE=CF=20米,斜坡AB的坡角∠A=30°,斜坡CD的坡度i=1:3,(坡度是指坡面的铅直高度与水平宽度的比).求坝底AD的宽.(结果保留整数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com