
一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其它两个顶点在矩形的边上,则剪下的等腰三角形的面积为多少平方厘米( )
A.50 B.50或40 C.50或40或30 D.50或30或20
C【考点】等腰三角形的性质;勾股定理;矩形的性质.
【专题】压轴题;分类讨论.
【分析】本题中由于等腰三角形的位置不确定,因此要分三种情况进行讨论求解,①如图(1),②如图(2),③如图(3),分别求得三角形的面积.
【解答】解:如图四边形ABCD是矩形,AD=18cm,AB=16cm;
本题可分三种情况:
①如图(1):△AEF中,AE=AF=10cm;
S△AEF=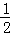 •AE•AF=50cm2;
•AE•AF=50cm2;

②如图(2):△AGH中,AG=GH=10cm;
在Rt△BGH中,BG=AB﹣AG=16﹣10=6cm;
根据勾股定理有:BH=8cm;
∴S△AGH=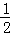 AG•BH=
AG•BH=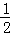 ×8×10=40cm2;
×8×10=40cm2;
③如图(3):△AMN中,AM=MN=10cm;
在Rt△DMN中,MD=AD﹣AM=18﹣10=8cm;
根据勾股定理有DN=6cm;
∴S△AMN=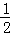 AM•DN=
AM•DN= ×10×6=30cm2.
×10×6=30cm2.
故选C.
【点评】本题主要考查了等腰三角形的性质、矩形的性质、勾股定理等知识,解题的关键在于能够进行正确的讨论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
将抛物线y=2(x﹣1)2+1向右平移1个单位长度,再向下移1个单位长度,所得的抛物线解析式为( )
A.y=2x2+1 B.y=2(x﹣2)2+2 C.y=2(x﹣2)2 D.y=2x2
查看答案和解析>>
科目:初中数学 来源: 题型:
美丽的雪花扮靓了我们可爱的家乡,但高速公路清雪刻不容缓.某高速公路维护站引进甲、乙两种型号的清雪车,已知甲型清雪车比乙型清雪车每天多清理路段6千米,甲型清雪车清理90千米与乙型清雪车清理60千米路段所用的时间相同.
(1)甲型、乙型清雪车每天各清理路段多少千米?
(2)此公路维护站欲购置甲、乙两种型号清雪车共20台,甲型每台30万元,乙型每台15万元,若在购款不超过360万元,甲型、乙型都购买的情况下,甲型清雪车最多可购买几台?
查看答案和解析>>
科目:初中数学 来源: 题型:
正方形ABCD边长为a,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图,则图中阴影部分的面积之和等于( )
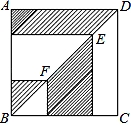
A.a2 B.0.25a2 C.0.5a2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
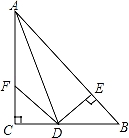
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF.说明:
(1)CD=EB;
(2)AB=AF+2EB.
查看答案和解析>>
科目:初中数学 来源: 题型:
我省2013年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2014年增速位居全国第一.若2015年的快递业务量达到4.5亿件,设2014年与201 5年这两年的平均增长率为x,则下列方程正确的是( )
5年这两年的平均增长率为x,则下列方程正确的是( )
A.1.4(1+x)=4.5 B.1.4(1+2x)=4.5
C.1.4(1+x)2=4.5 D.1.4(1+x)+1.4(1+x)2=4.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com