
【题目】将一个直角三角形纸片ABO放置在平面直角坐标系中,点 ![]() ,点B(0,1),点O(0,0).P是边AB上的一点(点P不与点A,B重合),沿着OP折叠该纸片,得点A的对应点A'.
,点B(0,1),点O(0,0).P是边AB上的一点(点P不与点A,B重合),沿着OP折叠该纸片,得点A的对应点A'.
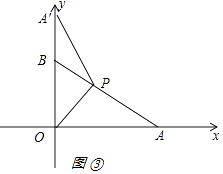
(1)如图①,当点A'在第一象限,且满足A'B⊥OB时,求点A'的坐标;
(2)如图②,当P为AB中点时,求A'B的长;
(3)当∠BPA'=30°时,求点P的坐标(直接写出结果即可).
【答案】
(1)
解:∵点 ![]() ,点B(0,1),
,点B(0,1),
∴OA= ![]() ,OB=1,
,OB=1,
由折叠的性质得:OA'=OA= ![]() ,
,
∵A'B⊥OB,
∴∠A'BO=90°,
在Rt△A'OB中,A'B= ![]() =
= ![]() ,
,
∴点A'的坐标为( ![]() ,1);
,1);
(2)
解:在Rt△ABO中,OA= ![]() ,OB=1,
,OB=1,
∴AB= ![]() =2,
=2,
∵P是AB的中点,
∴AP=BP=1,OP= ![]() AB=1,
AB=1,
∴OB=OP=BP
∴△BOP是等边三角形,
∴∠BOP=∠BPO=60°,
∴∠OPA=180°﹣∠BPO=120°,
由折叠的性质得:∠OPA'=∠OPA=120°,PA'=PA=1,
∴∠BOP+∠OPA'=180°,
∴OB∥PA',
又∵OB=PA'=1,
∴四边形OPA'B是平行四边形,
∴A'B=OP=1;
(3)
解:设P(x,y),分两种情况:
①如图③所示:点A'在y轴上,
在△OPA'和△OPA中, 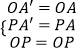 ,
,
∴△OPA'≌△OPA(SSS),
∴∠A'OP=∠AOP= ![]() ∠AOB=45°,
∠AOB=45°,
∴点P在∠AOB的平分线上,
设直线AB的解析式为y=kx+b,
把点 ![]() ,点B(0,1)代入得:
,点B(0,1)代入得: ![]() ,
,
解得: 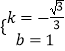 ,
,
∴直线AB的解析式为y=﹣ ![]() x+1,
x+1,
∵P(x,y),
∴x=﹣ ![]() x+1,
x+1,
解得:x= ![]() ,
,
∴P( ![]() ,
, ![]() );
);
②如图④所示:
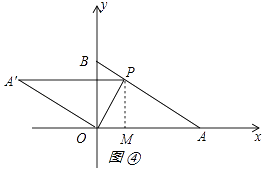
由折叠的性质得:∠A'=∠A=30°,OA'=OA,
∵∠BPA'=30°,
∴∠A'=∠A=∠BPA',
∴OA'∥AP,PA'∥OA,
∴四边形OAPA'是菱形,
∴PA=OA= ![]() ,作PM⊥OA于M,如图④所示:
,作PM⊥OA于M,如图④所示:
∵∠A=30°,
∴PM= ![]() PA=
PA= ![]() ,
,
把y= ![]() 代入y=﹣
代入y=﹣ ![]() x+1得:
x+1得: ![]() =﹣
=﹣ ![]() x+1,
x+1,
解得:x= ![]() ,
,
∴P( ![]() ,
, ![]() );
);
综上所述:当∠BPA'=30°时,点P的坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
【解析】(1)由点A和B的坐标得出OA= ![]() ,OB=1,由折叠的性质得:OA'=OA=
,OB=1,由折叠的性质得:OA'=OA= ![]() ,由勾股定理求出A'B=
,由勾股定理求出A'B= ![]() =
= ![]() ,即可得出点A'的坐标为(
,即可得出点A'的坐标为( ![]() ,1);(2)由勾股定理求出AB=
,1);(2)由勾股定理求出AB= ![]() =2,证出OB=OP=BP,得出△BOP是等边三角形,得出∠BOP=∠BPO=60°,求出∠OPA=120°,由折叠的性质得:∠OPA'=∠OPA=120°,PA'=PA=1,证出OB∥PA',得出四边形OPA'B是平行四边形,即可得出A'B=OP=1;(3)分两种情况:①点A'在y轴上,由SSS证明△OPA'≌△OPA,得出∠A'OP=∠AOP=
=2,证出OB=OP=BP,得出△BOP是等边三角形,得出∠BOP=∠BPO=60°,求出∠OPA=120°,由折叠的性质得:∠OPA'=∠OPA=120°,PA'=PA=1,证出OB∥PA',得出四边形OPA'B是平行四边形,即可得出A'B=OP=1;(3)分两种情况:①点A'在y轴上,由SSS证明△OPA'≌△OPA,得出∠A'OP=∠AOP= ![]() ∠AOB=45°,得出点P在∠AOB的平分线上,由待定系数法求出直线AB的解析式为y=﹣
∠AOB=45°,得出点P在∠AOB的平分线上,由待定系数法求出直线AB的解析式为y=﹣ ![]() x+1,即可得出点P的坐标;②由折叠的性质得:∠A'=∠A=30°,OA'=OA,作出四边形OAPA'是菱形,得出PA=OA=
x+1,即可得出点P的坐标;②由折叠的性质得:∠A'=∠A=30°,OA'=OA,作出四边形OAPA'是菱形,得出PA=OA= ![]() ,作PM⊥OA于M,由直角三角形的性质求出PM=
,作PM⊥OA于M,由直角三角形的性质求出PM= ![]() PA=
PA= ![]() ,把y=
,把y= ![]() 代入y=﹣
代入y=﹣ ![]() x+1求出点P的纵坐标即可.
x+1求出点P的纵坐标即可.
【考点精析】本题主要考查了勾股定理的概念和翻折变换(折叠问题)的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( ) 
A.121
B.362
C.364
D.729
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,且AD=12cm.点P从点A出发,以3cm/s的速度在射线AD上运动;同时,点Q从点C出发,以1cm/s的速度在射线CB上运动.运动时间为t,当t=______秒(s)时,点P、Q、C、D构成平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中第九卷《勾股》主要讲述了以测量问题为中心的直角三角形三边互求,之中记载了一道有趣的“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”
译文:“今有正方形水池边长为1丈,有棵芦苇生长在它长出水面的部分为1尺.将芦苇的中央,向池岸牵引,恰好与水岸齐接.问水深,芦苇的长度分别是多少尺?”(备注:1丈=10尺)
如果设水深为![]() 尺,那么芦苇长用含
尺,那么芦苇长用含![]() 的代数式可表示为_______尺,根据题意,可列方程为______________.
的代数式可表示为_______尺,根据题意,可列方程为______________.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解中学生获取信息的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,根据调查的结果绘制条形图如图,该调查的方式和图中a的值分别是( )

A. 抽样调查,24 B. 普查,24 C. 抽样调查,26 D. 普查,26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了分析九年级学生艺术考试的成绩,随机抽查了两个班级的各5名学生的成绩,它们分别是:
九(1)班:96,92,94,97,96
九(2)班:90,98,97,98,92
通过数据分析,列表如下:

(1)![]()
(2)计算两个班级所抽取的学生艺术成绩的方差,判断哪个班学生艺术成绩比较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于两点
轴交于两点![]() 和
和![]() 与
与![]() 轴交于点
轴交于点![]() 动点
动点![]() 沿
沿![]() 的边
的边![]() 以每秒
以每秒![]() 个单位长度的速度由起点
个单位长度的速度由起点![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 的另一边
的另一边![]() 于点
于点![]() 将
将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,设点
处,设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.

(1)求抛物线的解析式;
(2)N为抛物线上的点(点![]() 不与点
不与点![]() 重合)且满足
重合)且满足![]() 直接写出
直接写出![]() 点的坐标;
点的坐标;
(3)是否存在某一时刻![]() ,使
,使![]() 的面积最大,若存在,求出
的面积最大,若存在,求出![]() 的值和最大面积;若不存在,请说明理由.
的值和最大面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com